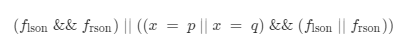leetcode算法-树

leetcode算法

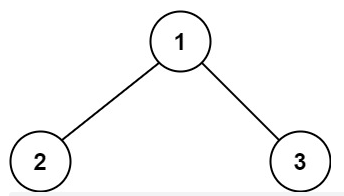
(LeetCode-94) 二叉树的中序遍历

题目

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

1 2	输入：root = [1,null,2,3] 输出：[1,3,2]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [1] 输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

代码

public class InorderTraversal {

    public static void main(String[] args) {
        MyTreeNode nodei = new MyTreeNode(9);
        MyTreeNode nodeh = new MyTreeNode(8);
        MyTreeNode nodeg = new MyTreeNode(7);
        MyTreeNode nodef = new MyTreeNode(6);
        MyTreeNode nodee = new MyTreeNode(5, null, nodei);
        MyTreeNode noded = new MyTreeNode(4, nodeg ,nodeh);
        MyTreeNode nodec = new MyTreeNode(3,nodee,nodef);
        MyTreeNode nodeb = new MyTreeNode(2,noded,null);
        MyTreeNode nodea = new MyTreeNode(1, nodeb, nodec);
        List<MyTreeNode> list =  inorderTraversal(nodea);
        for(MyTreeNode node : list ){
            System.out.println(node.val);
        }
    }

    // 递归
//    public static List<MyTreeNode> inorderTraversal(MyTreeNode root) {
//        List<MyTreeNode> list = new ArrayList<MyTreeNode>();
//        accessTree(root, list);
//        return list;
//    }
//
//    public static void accessTree(MyTreeNode root, List<MyTreeNode> res) {
//        if(root == null){
//            return ;
//        }
//        if(root.left != null){
//            accessTree( root.left, res);
//        }
//        res.add(root);
//        if(root.right != null){
//            accessTree( root.right, res);
//        }
//    }

    // 迭代
    public static List<MyTreeNode> inorderTraversal(MyTreeNode root) {
        List<MyTreeNode> list = new ArrayList<MyTreeNode>();
        Stack<MyTreeNode> stack = new Stack<MyTreeNode>();
        while (root != null || !stack.isEmpty()){
            while (root != null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            list.add(root);
            root = root.right;
        }
        return list;
    }
}

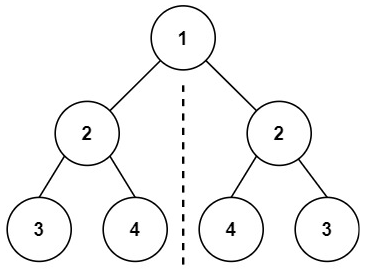
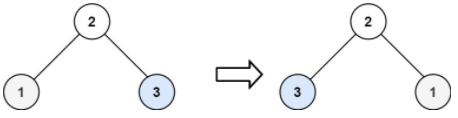
(LeetCode-101) 对称二叉树

题目

给你一个二叉树的根节点 root ，检查它是否轴对称

示例 1：

1 2	输入：root = [1,2,2,3,4,4,3] 输出：true

示例 2：

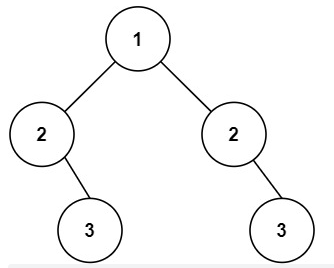
1 2	输入：root = [1,2,2,null,3,null,3] 输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

代码

class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
public class Symmetric {
    public static void main(String[] args) {
//        TreeNode nodei = new TreeNode(9);
//        TreeNode nodeh = new TreeNode(8);
        TreeNode nodeg = new TreeNode(5);
        TreeNode nodef = new TreeNode(4);
        TreeNode nodee = new TreeNode(5);
        TreeNode noded = new TreeNode(4);
        TreeNode nodec = new TreeNode(2,nodef,nodeg);
        TreeNode nodeb = new TreeNode(2,noded,nodee);
        TreeNode nodea = new TreeNode(1, nodeb, nodec);
        System.out.println(isSymmetric(nodea));
    }
    public static boolean isSymmetric(TreeNode root) {
        if(root == null){
            return false;
        }
        if(!deepCheck(root.left, root.right)) {
            return false;
        }
        return true;
    }

    public static boolean deepCheck(TreeNode left, TreeNode right) {
        if(left == null && right == null){
            return true;
        }
        if(left == null || right == null){
            return false;
        }
        if(left.val != right.val){
            return false;
        }
        return deepCheck(left.left, right.right) && deepCheck(left.right, right.left);
    }
}

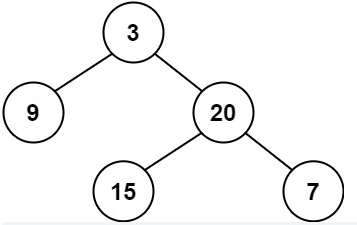
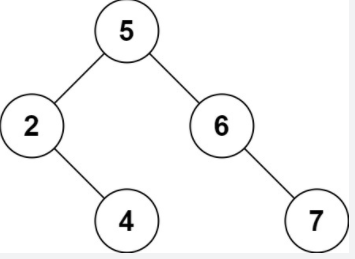
(LeetCode-110) 平衡二叉树

题目

给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

1 2	输入：root = [3,9,20,null,null,15,7] 输出：true

示例 2：

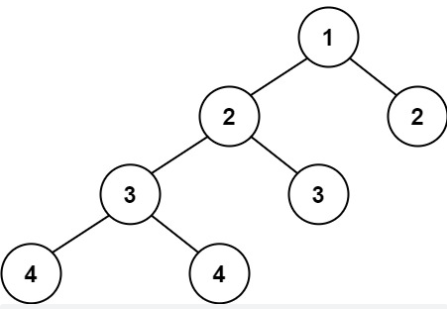
1 2	输入：root = [1,2,2,3,3,null,null,4,4] 输出：false

示例 3：

1 2	输入：root = [] 输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

分析

平衡二叉树要求的是左右子节点的高度不能超过1，所以我们可以判断树的左右两个子节点的高度只要不超过1就行，而树的高度怎么计算呢，其实很简单，代码如下

//计算树中节点的高度
public int depth(TreeNode root) {
    if (root == null)
        return 0;
    return Math.max(depth(root.left), depth(root.right)) + 1;
}

代码

public class BalancedTree {

    public static void main(String[] args) {
        TreeNode nodeg = new TreeNode(5);
        TreeNode nodef = new TreeNode(4);
        TreeNode nodee = new TreeNode(5);
        TreeNode noded = new TreeNode(4);
        TreeNode nodec = new TreeNode(2,nodef,nodeg);
        TreeNode nodeb = new TreeNode(2,noded,nodee);
        TreeNode nodea = new TreeNode(1, nodeb, nodec);
        System.out.println(isBalanced(nodea));
    }
    public static boolean isBalanced(TreeNode root) {
       if(root == null){
           return true;
       }
       return helper(root) != -1;
    }

    public static int helper(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = helper((root.left));
        int right = helper((root.right));
        if(left == -1 || right == -1 || Math.abs(left - right) > 1){
            return -1;
        }
        return Math.max(left , right) + 1;
    }
}

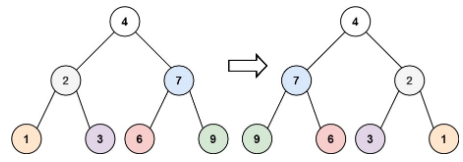
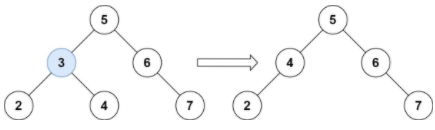
(LeetCode-226) 翻转二叉树

题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

1 2	输入：root = [4,2,7,1,3,6,9] 输出：[4,7,2,9,6,3,1]

示例 2：

1 2	输入：root = [2,1,3] 输出：[2,3,1]

示例 3：

1 2	输入：root = [] 输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

代码

public class InvertTree {
    public static void main(String[] args) {
        TreeNode nodeg = new TreeNode(9);
        TreeNode nodef = new TreeNode(6);
        TreeNode nodee = new TreeNode(3);
        TreeNode noded = new TreeNode(1);
        TreeNode nodec = new TreeNode(7,nodef,nodeg);
        TreeNode nodeb = new TreeNode(2,noded,nodee);
        TreeNode nodea = new TreeNode(4, nodeb, nodec);
        nodea = invertTree(nodea);
        System.out.println(nodea.val);
    }

    public static TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        TreeNode temp = root.left ;
        root.left = root.right;
        root.right = temp;
        invertTree( root.left);
        invertTree( root.right);
        return root;
    }
}

(LeetCode-208) 实现 Trie (前缀树)

题目

Trie（发音类似 “try”）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

分析

方法

要解决这个题目，首先要搞明白什么是Trie树。

Trie树

即字典树，也有的称为前缀树，是一种树形结构。广泛应用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

先看一下几个场景问题：

1.我们输入n个单词，每次查询一个单词，需要回答出这个单词是否在之前输入的n单词中出现过。
答：当然是用map来实现。

2.我们输入n个单词，每次查询一个单词的前缀，需要回答出这个前缀是之前输入的n单词中多少个单词的前缀？
答：还是可以用map做，把输入n个单词中的每一个单词的前缀分别存入map中，然后计数，这样的话复杂度会非常的高。若有n个单词，平均每个单词的长度为c，那么复杂度就会达到nc。

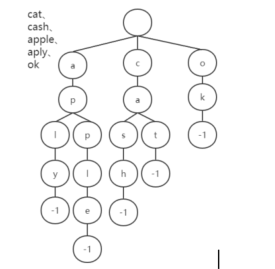
因此我们需要更加高效的数据结构，这时候就是Trie树的用武之地了。现在我们通过例子来理解什么是Trie树。现在我们对cat、cash、apple、aply、ok这几个单词建立一颗Trie树。

从图中可以看出：

1.每一个节点代表一个字符
2.有相同前缀的单词在树中就有公共的前缀节点。
3.整棵树的根节点是空的。
4.每个节点结束的时候用一个特殊的标记来表示，这里我们用-1来表示结束，从根节点到-1所经过的所有的节点对应一个英文单词。
5.查询和插入的时间复杂度为O(k)，k为字符串长度，当然如果大量字符串没有共同前缀时还是很耗内存的。

理解了Trie树以后，代码实现就很简单了，既可以用数组实现，也可以用Map实现。

代码

public class Trie {
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }

    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }

    public boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    private Trie searchPrefix(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            char ch = prefix.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                return null;
            }
            node = node.children[index];
        }
        return node;
    }
}

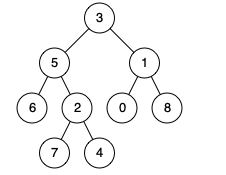
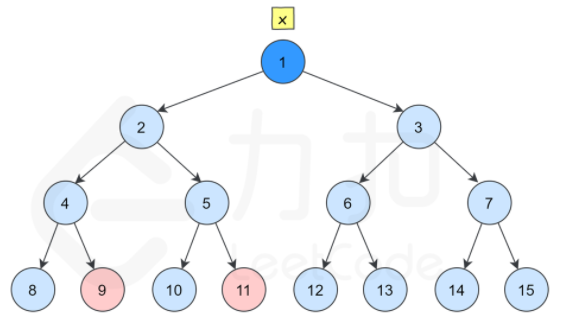
(LeetCode-236) 二叉树的最近公共祖先

题目

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

1
2
3

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

1
2
3

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

1 2	输入：root = [1,2], p = 1, q = 2 输出：1

分析

方法

思路和算法

我们递归遍历整棵二叉树，定义 fx 表示 x 节点的子树中是否包含 p 节点或 q 节点，如果包含为 true，否则为 false。那么符合条件的最近公共祖先 x 一定满足如下条件：

其中 lson 和 rson 分别代表 x 节点的左孩子和右孩子。初看可能会感觉条件判断有点复杂，我们来一条条看，

flson && frson说明左子树和右子树均包含 p 节点或 q 节点，如果左子树包含的是 p 节点，那么右子树只能包含 q 节点，反之亦然，因为p 节点和 q 节点都是不同且唯一的节点，因此如果满足这个判断条件即可说明 x 就是我们要找的最近公共祖先
再来看第二条判断条件，这个判断条件即是考虑了 x 恰好是 p 节点或 q 节点且它的左子树或右子树有一个包含了另一个节点的情况，因此如果满足这个判断条件亦可说明 x 就是我们要找的最近公共祖先。

你可能会疑惑这样找出来的公共祖先深度是否是最大的。其实是最大的，因为我们是自底向上从叶子节点开始更新的，所以在所有满足条件的公共祖先中一定是深度最大的祖先先被访问到，且由于 fx 本身的定义很巧妙，在找到最近公共祖先 x 以后, fx 按定义被设置为 true ，即假定了这个子树中只有一个 p 节点或 q 节点，因此其他公共祖先不会再被判断为符合条件。

下图展示了一个示例，搜索树中两个节点 9 和 11 的最近公共祖先。

代码

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

public class LowestCommonAncestor {
    public static void main(String[] args) {
        TreeNode node7 = new TreeNode(7);
        TreeNode node4 = new TreeNode(4);
        TreeNode node0 = new TreeNode(0);
        TreeNode node8 = new TreeNode(8);
        TreeNode node6 = new TreeNode(6);
        TreeNode node2 = new TreeNode(2, node7, node4);
        TreeNode node5 = new TreeNode(5, node6, node2);
        TreeNode node1 = new TreeNode(1, node0, node8);
        TreeNode node3 = new TreeNode(3, node5, node1);
        TreeNode node = new LowestCommonAncestor().lowestCommonAncestor(node3, node5, node4);
        System.out.println("");
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 找到p 或q 所在节点， 终止递归； 或者找到叶子节点也没有找到q 或 q
        if(root == null || root == p || root == q) return root;
        // 返回时left和right 的返回结果是p或者q 或者为null， 或者p 和q的公共祖先node
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        // left 和 right 不为空， 说明p和q就在当前节点下， 当前节点就是我们需要的最近公共祖先
        if(left != null && right != null) return root;
        // left 和 right 有一个为空， 返回不为空的那个
        // left 和right 的都为空， 返回哪个都可以， 这里统一返回right
        return left != null ? left : right;
    }
}

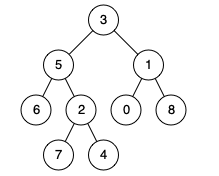
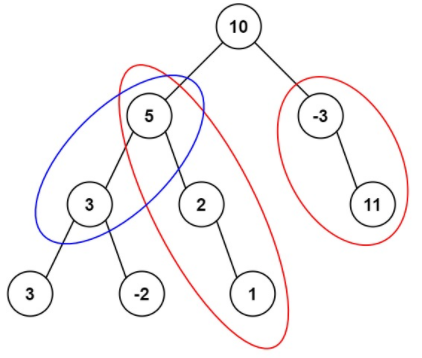
(LeetCode-437)路径总和 III

题目

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

1
2
3

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

1 2	输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：3

分析

方法一：深度优先搜索

思路与算法

我们首先想到的解法是穷举所有的可能，我们访问每一个节点 node，检测以 node 为起始节点且向下延深的路径有多少种。我们递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。

我们首先定义 rootSum(p,val) 表示以节点 p 为起点向下且满足路径总和为 valval 的路径数目。我们对二叉树上每个节点 p 求出 rootSum(p,targetSum)，然后对这些路径数目求和即为返回结果。
我们对节点 p 求 rootSum(p,targetSum) 时，以当前节点 p 为目标路径的起点递归向下进行搜索。假设当前的节点 p 的值为 val，我们对左子树和右子树进行递归搜索，对节点 p 的左孩子节点 pl 求出 rootSum(pl,targetSum−val)，以及对右孩子节点 pr 求出 rootSum(pr,targetSum−val)。节点 p 的rootSum(p,targetSum) 即等于 rootSum(pl,targetSum−val) 与 rootSum(pr,targetSum−val) 之和，同时我们还需要判断一下当前节点 p 的值是否刚好等于 targetSum。
我们采用递归遍历二叉树的每个节点 p，对节点 p 求 rootSum(p,val)，然后将每个节点所有求的值进行相加求和返回。

代码

// 暴力
public int pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return 0;
        }

        int ret = rootSum(root, targetSum);
        ret += pathSum(root.left, targetSum);
        ret += pathSum(root.right, targetSum);
        return ret;
    }

    public int rootSum(TreeNode root, int targetSum) {
        int ret = 0;

        if (root == null) {
            return 0;
        }
        int val = root.val;
        if (val == targetSum) {
            ret++;
        } 

        ret += rootSum(root.left, targetSum - val);
        ret += rootSum(root.right, targetSum - val);
        return ret;
    }

// 前缀和
 public int pathSum(TreeNode root, int targetSum) {
        Map<Long, Integer> prefix = new HashMap<Long, Integer>();
        prefix.put(0L, 1);
        return dfs(root, prefix, 0, targetSum);
    }

    public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
        if (root == null) {
            return 0;
        }

        int ret = 0;
        curr += root.val;

        ret = prefix.getOrDefault(curr - targetSum, 0);
        prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);
        ret += dfs(root.left, prefix, curr, targetSum);
        ret += dfs(root.right, prefix, curr, targetSum);
        prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);

        return ret;
    }

(LeetCode-450) 删除二叉搜索树中的节点

题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

1
2
3

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

1 2	输入: root = [], key = 0 输出: []

分析

方法一：递归

思路

二叉搜索树有以下性质：

左子树的所有节点（如果有）的值均小于当前节点的值；
右子树的所有节点（如果有）的值均大于当前节点的值；
左子树和右子树均为二叉搜索树。

二叉搜索树的题目往往可以用递归来解决。此题要求删除二叉树的节点，函数 deleteNode 的输入是二叉树的根节点 root 和一个整数 key，输出是删除值为 key 的节点后的二叉树，并保持二叉树的有序性。可以按照以下情况分类讨论：

root 为空，代表未搜索到值为 key 的节点，返回空。
root.val>key，表示值为 key 的节点可能存在于 root 的左子树中，需要递归地在 root.left 调用 deleteNode，并返回 root。
root.val<key，表示值为 key 的节点可能存在于 root 的右子树中，需要递归地在 root.right 调deleteNode，并返回 root。
root.val=key，root 即为要删除的节点。此时要做的是删除 root，并将它的子树合并成一棵子树，保持有序性，并返回根节点。根据 root 的子树情况分成以下情况讨论：
- root 为叶子节点，没有子树。此时可以直接将它删除，即返回空。
- root 只有左子树，没有右子树。此时可以将它的左子树作为新的子树，返回它的左子节点。
- root 只有右子树，没有左子树。此时可以将它的右子树作为新的子树，返回它的右子节点。
- root 有左右子树，这时可以将 root 的后继节点（比 root 大的最小节点，即它的右子树中的最小节点，记为 successor）作为新的根节点替代 root，并将 successor 从 root 的右子树中删除，使得在保持有序性的情况下合并左右子树。
  
  简单证明，successor 位于 root 的右子树中，因此大于root 的所有左子节点；successor 是 root 的右子树中的最小节点，因此小于 root 的右子树中的其他节点。以上两点保持了新子树的有序性。
  
  在代码实现上，我们可以先寻找 successor，再删除它。successor 是 root 的右子树中的最小节点，可以先找到 root 的右子节点，再不停地往左子节点寻找，直到找到一个不存在左子节点的节点，这个节点即为 successor。然后递归地在root.right 调用 deleteNode 来删除 successor。因为 successor 没有左子节点，因此这一步递归调用不会再次步入这一种情况。然后将 successor 更新为新的 root 并返回。

代码

public class DeleteNode {
    public static void main(String[] args) {
        TreeNode node9 = new TreeNode(38);
        TreeNode node8 = new TreeNode(48);
        TreeNode node7 = new TreeNode(70);
        TreeNode node4 = new TreeNode(40, node9, node8);
        TreeNode node6 = new TreeNode(60, node7, null);
        TreeNode node2 = new TreeNode(20);
        TreeNode node3 = new TreeNode(30, node2, node4);
        TreeNode node5 = new TreeNode(50, node3, node6);
        new DeleteNode().deleteNode(node5, 30);
        System.out.println("");
    }
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        if (root.val > key) {
            root.left = deleteNode(root.left, key);
            return root;
        }
        if (root.val < key) {
            root.right = deleteNode(root.right, key);
            return root;
        }
        if (root.val == key) {
            if (root.left == null && root.right == null) {
                return null;
            }
            if (root.right == null) {
                return root.left;
            }
            if (root.left == null) {
                return root.right;
            }
            TreeNode successor = root.right;
            while (successor.left != null) {
                successor = successor.left;
            }
            root.right = deleteNode(root.right, successor.val);
            successor.right = root.right;
            successor.left = root.left;
            return successor;
        }
        return root;
    }
}

(LeetCode-538) 把二叉搜索树转换为累加树

题目

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

分析

二叉搜索树的中序遍历是一个单调递增的有序序列。如果我们反序地中序遍历该二叉搜索树，即可得到一个单调递减的有序序列。

方法一：反序中序遍历

思路及算法

本题中要求我们将每个节点的值修改为原来的节点值加上所有大于它的节点值之和。这样我们只需要反序中序遍历该二叉搜索树，记录过程中的节点值之和，并不断更新当前遍历到的节点的节点值，即可得到题目要求的累加树。

代码

public class ConvertBST {
    public static void main(String[] args) {
        TreeNode node5 = new TreeNode(5);
        TreeNode node8 = new TreeNode(8);
        TreeNode node7 = new TreeNode(7, null, node8);
        TreeNode node3 = new TreeNode(3);
        TreeNode node0 = new TreeNode(0);
        TreeNode node6 = new TreeNode(6, node5, node7);
        TreeNode node2 = new TreeNode(2, null, node3);
        TreeNode node1 = new TreeNode(1, node0, node2);
        TreeNode node4 = new TreeNode(4, node1, node6);
        new ConvertBST().convertBST(node4);
        System.out.println("");
    }

    int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root == null){
            return null;
        }
        convertBST(root.right);
        sum += root.val;
        root.val = sum;
        convertBST(root.left);
        return root;
    }
}

(LeetCode-543) 二叉树的直径

题目

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

分析

方法

通过示例，我们能够看到，一棵二叉树里两个结点路径长度中的最大值，其实就是树的左右子树中深度最大的两个子节点的路径，所以可以通过不断寻找左右子树中最深的节点来解决这个问题。

代码

int max = 0;
   public int diameterOfBinaryTree(TreeNode root) {
       depth(root);
       return 0;
   }
   private int depth(TreeNode root) {
       if(root == null) return 0;
       int left = depth(root.left);
       int right = depth(root.right);
       max = Math.max(max, left + right);
       return Math.max(left, right) + 1;
   }

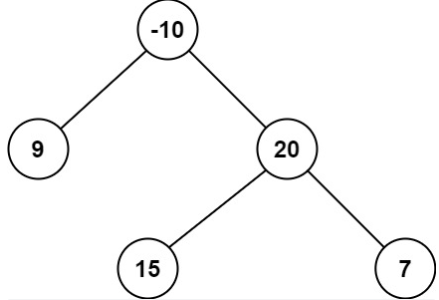
(LeetCode-124) 二叉树中的最大路径和

题目

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

1
2
3

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

1
2
3

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

分析

代码

public class MaxPathSum {
    public static void main(String[] args) {
        TreeNode node3 = new TreeNode(-1);
        TreeNode node5 = new TreeNode(2, node3, null);
        new MaxPathSum().maxPathSum(node5);
        System.out.println(max);
    }

    public int maxPathSum(TreeNode root) {
        deptSum( root);
        return max;
    }

     static int max = Integer.MIN_VALUE;
    public int deptSum(TreeNode root) {
        if(root == null) return 0;
        int left = Math.max(deptSum(root.left), 0) ;
        int right = Math.max(deptSum(root.right), 0) ;
        max = Math.max(max, left + right + root.val);
        return Math.max(left, right) + root.val;
    }
}

(LeetCode-94) 二叉树的中序遍历

题目

代码

(LeetCode-101) 对称二叉树

题目

代码

(LeetCode-110) 平衡二叉树

题目

分析

代码

(LeetCode-226) 翻转二叉树

题目

代码

(LeetCode-208) 实现 Trie (前缀树)

题目

分析

方法

Trie树

代码

(LeetCode-236) 二叉树的最近公共祖先

题目

分析

方法

代码

(LeetCode-437)路径总和 III

题目

分析

方法一：深度优先搜索

代码

(LeetCode-450) 删除二叉搜索树中的节点

题目

分析

方法一：递归

代码

**(LeetCode-538) **把二叉搜索树转换为累加树

题目

分析

方法一：反序中序遍历

代码

**(LeetCode-543) **二叉树的直径

题目

分析

方法

代码

**(LeetCode-124) **二叉树中的最大路径和

题目

分析

代码

(LeetCode-538) 把二叉搜索树转换为累加树

(LeetCode-543) 二叉树的直径

(LeetCode-124) 二叉树中的最大路径和