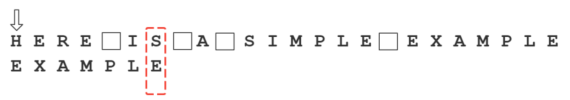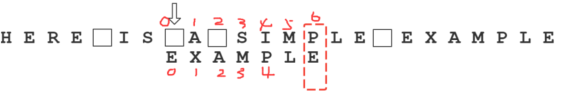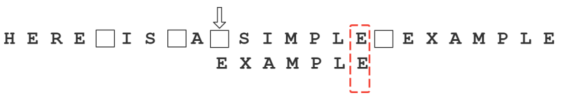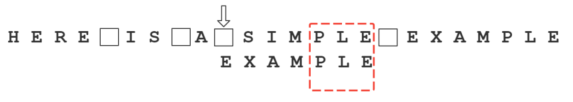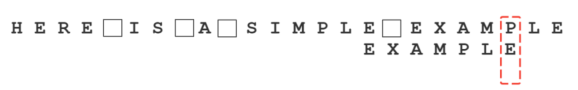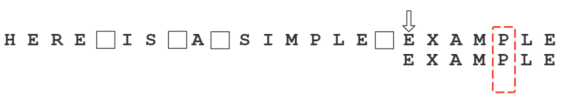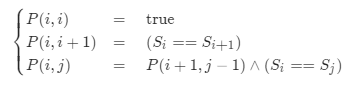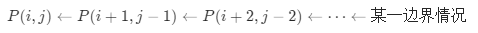leetcode算法
(LeetCode-20) 有效的括号 题目 给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
示例 2:
示例 3:
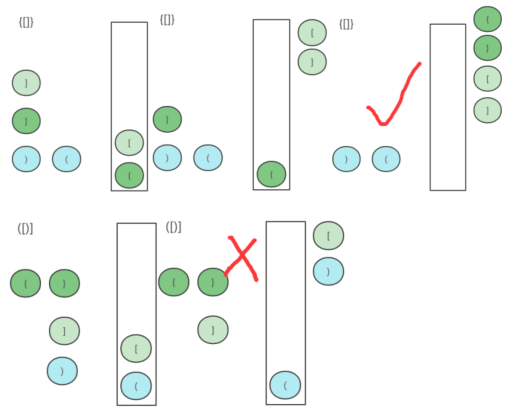
分析 方法 仔细分析,可以看到,每当遇到一个右括号,不管是’)’,’}’,’]’ ,表示需要前面一个有匹配的左括号,而且如果左右括号没有相邻在一起,就需要左右括号之间的其他括号也符合上一个原则。
通过分析过程,我们是否可以得到什么提示?需要按顺序往前回溯曾经处理的数据,是不是有点先进后出的感觉。所以可以利用栈来处理这个题目。这个题目其实和我们一期——栈与队列——(LeetCode-394)字符串解码这个题目有非常大的相似之处,只是这个题目更简单。
在具体的代码实现上,是入栈左括号还是右括号都是可以的,这个没有什么区别。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class IsValidStr { public static void main(String[] args) { String s = "(]"; System.out.println(isValid(s)); } public static boolean isValid(String s) { Stack<Character> stack = new Stack<>(); for(char c : s.toCharArray()){ if(c == '(' ){ stack.push(')'); }else if (c == '{'){ stack.push('}'); }else if(c == '['){ stack.push(']'); }else if(c == ')' || c == ']' || c == '}' ) { if(stack.isEmpty() || !stack.pop().equals(c)){ return false; } } } return stack.isEmpty(); } }
**(LeetCode-415) **字符串相加 题目 给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
1 2 输入:num1 = "11", num2 = "123" 输出:"134"
示例 2:
1 2 输入:num1 = "456", num2 = "77" 输出:"533"
示例 3:
1 2 输入:num1 = "0", num2 = "0" 输出:"0"
分析 方法 这个问题虽然题目要求不能直接将输入的字符串转换为整数形式,但是并没有禁止把字符串拆开成一个个的字符后,我们手动累加。
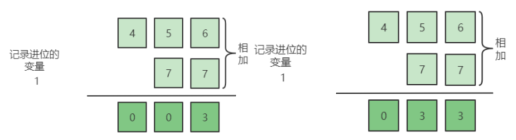
所以我们可以仿照小时候学习整数相加列竖式的办法,一个个字符对齐位以后再相加,同时在相加的顺序上注意需要逆序处理,因为我们整数的相加就是从个十百位这样的顺序相加的。因为可能有进位的情况,所以我们还需要一个变量专门用来记录是否进位以及进位的数量。理解上面的意思,这个代码就很简单了。
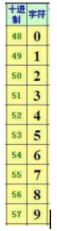
至于获得字符串中每个字符,怎么把他转为数字呢?可以利用acsii码表,将字符减去’0’,就是这个字符所代表的数字
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class AddStrings { public static void main(String[] args) { String num1 = "456", num2 = "77"; System.out.println(addStrings(num1, num2)); } public static String addStrings(String num1, String num2) { StringBuilder sb = new StringBuilder(); // 记录进位的变量 int carry = 0; for(int i = num1.length() - 1, j = num2.length() -1; i >= 0 || j >= 0 || carry == 1; i--, j--){ int x = i < 0 ? 0 : num1.charAt(i) - '0'; int y = j < 0 ? 0 : num2.charAt(j) - '0'; sb.append((x + y + carry) % 10); carry = (x + y + carry) / 10; } return sb.reverse().toString(); } }
字符串匹配之BF算法 在一个字符串中寻找另一字符串,最容易想到的,也是最简单的办法是:取主串和模式串/搜索串中的每一位依次比较,如果匹配则同时后移一位继续比较,直至匹配到模式串的最后一位;如果出现不匹配的字符,则模式串向后移动一位,继续比较。这种解决问题的思路简单暴力,也是这个算法被叫做BF(Brute Force)的原因。
整个匹配的过程可以参考下图,我们假设主串为“abdea”,搜索串为“dea”:
这个算法的复杂度还是比较好分析的,我们假设主串的长度是 m,模式串的长度是 n,在最好的情况下,在第一个字符处的匹配就能够成功,例如主串是 a b c d ,模式串是a b c,这时只遍历了模式串的长度,因为时间复杂度是 O(n);
在最坏的情况下,每次都需要遍历整个模式串,但是又未能匹配成功,例如主串是 a a a a a …a,模式串是 a a a a b,所以需要遍历 m - n + 1 次,时间复杂度是 O(m * n) 。
BF算法的最坏时间复杂度虽然不好,但它易于理解和编程,在实际应用中,一般还能达到近似于O(m+n)的时间度(最坏情况不是那么容易出现的),因此,还在被大量使用。
字符串匹配之BM算法 各种文本编辑器的”查找”功能(Ctrl+F),大多采用Boyer[ˈbɔɪə]-Moore[mʊə]算法。
Boyer-Moore算法不仅效率高,而且构思巧妙,容易理解。1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法。BM算法里的总体思路是:对于每一次失败的匹配尝试,算法都能够使用这些信息来排除尽可能多的无法匹配的位置。
下面根据Moore教授自己的例子来解释这种算法。
假定字符串为”HERE IS A SIMPLE EXAMPLE”,搜索词为”EXAMPLE”。
首先,”字符串”与”搜索词”头部对齐,从尾部开始比较。
这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。
我们看到,”S”与”E”不匹配。这时,”S”就被称为”坏字符”(bad character),即不匹配的字符。我们还发现,”S”不包含在搜索词”EXAMPLE”之中,这意味着可以把搜索词直接移到”S”的后一位。
依然从尾部开始比较,发现”P”与”E”不匹配,所以”P”是”坏字符”。但是,”P”包含在搜索词”EXAMPLE”之中。所以,将搜索词后移两位,两个”P”对齐。
我们由此总结出”坏字符规则”:
1 后移位数 = 坏字符的位置 – 模式串中的上一次出现位置
如果”坏字符”不包含在搜索词之中,则上一次出现位置为 -1。
以”P”为例,它作为”坏字符”,出现在主串的第6位(从0开始编号),也就是“空格,A,空格,S,I,M,P”,在模式串中的上一次出现位置为4,所以后移 6 - 4 = 2位。
再以前面第二步的”S”为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个模式串后移 6 - (-1) = 7位。
依然从尾部开始比较,”E”与”E”匹配。
比较前面一位,”LE”与”LE”匹配。
比较前面一位,”PLE”与”PLE”匹配。
比较前面一位,”MPLE”与”MPLE”匹配。我们把这种情况称为”好后缀”(good suffix),即所有尾部匹配的字符串。注意,”MPLE”、”PLE”、”LE”、”E”都是好后缀。
比较前一位,发现”I”与”A”不匹配。所以,”I”是”坏字符”。
根据”坏字符规则”,此时模式串应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?
我们知道,此时存在”好后缀”。所以,可以采用”好后缀规则”:
1 后移位数 = 好后缀的位置 – 模式串中的上一次出现位置
举例来说,如果字符串”ABCDAB”的后一个”AB”是”好后缀”。那么它的位置是5(从0开始计算,取最后的”B”的值),在模式串中的上一次出现位置是1(第一个”B”的位置),所以后移 5 - 1 = 4位,前一个”AB”移到后一个”AB”的位置。
再举一个例子,如果字符串”ABCDEF”的”EF”是好后缀,则”EF”的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个模式串移到”F”的后一位。
这个规则有三个注意点:
1 2 3 (1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。 (2)如果"好后缀"在模式串中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。 (3)如果"好后缀"有多个,如果最长的那个"好后缀"在模式串中只出现一次,其他"好后缀"的上一次出现位置必须在头部。比如我们的例子中所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。
可以看到,”坏字符规则”只能移3位,”好后缀规则”可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。
更巧妙的是,这两个规则的移动位数,只与模式串有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了
继续从尾部开始比较,”P”与”E”不匹配,因此”P”是”坏字符”。根据”坏字符规则”,后移 6 - 4 = 2位。
从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据”好后缀规则”,后移 6 - 0 = 6位,即头部的”E”移到尾部的”E”的位置。
最坏情况下找到模式所有出现的时间复杂度为O(mn),在最好情况下执行匹配找到模式所有出现的时间复杂度为O(n/m)。
所以,BM算法里的总体思路就是:对于每一次失败的匹配尝试,算法都能够使用这些信息来排除尽可能多的无法匹配的位置。同时可以预先计算生成《坏字符规则表》和《好后缀规则表》,大大加快查找匹配的速度。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 public class BMStr { public static void main(String[] args) { String main = "HERE IS A SIMPLE EXAMPLE"; // String main = "HEREXAMPLE"; String ptn = "EXAMPLE"; // String ptn = "abcab"; System.out.println(bm(main, ptn)); } /** * 生成好后缀数组 */ private static void goodSuffixRule(String str, int[] suffix, boolean[] prefix){ Arrays.fill(suffix, -1); Arrays.fill(prefix, false); int n = str.length(); for (int i = 0; i < n - 1; i++){ int j = i; int k = 0; while (j >= 0 && str.charAt(j) == str.charAt(n - k - 1)){ --j; ++k; suffix[k] = j + 1; } if (j == -1){ prefix[k] = true; } } } private static final int[] badChar = new int[256]; public static int bm(String main, String ptn){ if (main == null || ptn == null){ return -1; } int m = main.length(); int n = ptn.length(); badCharRule(ptn, badChar); int[] suffix = new int[n]; boolean[] prefix = new boolean[n]; goodSuffixRule(ptn, suffix, prefix); int i = n - 1; while (i <= m - 1) { int j = n - 1; while (j >= 0 && main.charAt(i) == ptn.charAt(j)){ --i; if (--j == -1){ return i + 1; } } //计算坏字符规则下移动的位数 int moveWithBC = j - badChar[main.charAt(i)]; //计算好后缀规则下移动的位数 int moveWithGS = Integer.MIN_VALUE; if (j < n - 1){ moveWithGS = moveWithGS(n, j, suffix, prefix); } i += Math.max(moveWithBC, moveWithGS); } return -1; } /** * 生成坏字符数组 */ private static void badCharRule(String str, int[] badChar){ Arrays.fill(badChar, -1); for (int i = 0; i < str.length(); i++) { badChar[str.charAt(i)] = i; } } /** * 计算好后缀情况下的移动位数 */ private static int moveWithGS(int n, int j, int[] suffix, boolean[] prefix){ int k = n - j - 1; if (suffix[k] != -1){ return j - suffix[k] + 1; } for (int i = k - 1; i >= 0; i--) { if (prefix[i]){ return n - i; } } return n; } }
(LeetCode- 3) 无重复字符的最长子串 题目 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
1 2 3 输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
1 2 3 输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
1 2 3 4 输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
分析 思路:
什么是滑动窗口?
其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求。所以,我们要移动这个队列!
如何移动?
我们只要把队列的左边的元素移出就行了,直到满足题目要求!
一直维持这样的队列,找出队列出现最长的长度时候,求出解!
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 public class LengthOfLongestSubstring { public static void main(String[] args) { String str = "pwwkew"; int max = new LengthOfLongestSubstring().lengthOfLongestSubstring(str); System.out.println(); } public int lengthOfLongestSubstring(String s) { Map<Character, Integer> map = new HashMap<>(); int start = 0, max = 0; for(int end = 0; end < s.length(); end++){ Integer index = map.get(s.charAt(end)); if(index != null){ start = Math.max(index + 1, start); } map.put(s.charAt(end), end); max = Math.max(max, end - start + 1); } return max; } // 从头开始判断当前最多有几个不重复串 public int lengthOfLongestSubstring(String s) { // 记录每个字符是否出现过 Set<Character> occ = new HashSet<Character>(); int n = s.length(); int rk = -1, ans = 0; for(int i = 0; i < n; ++i){ if(i != 0){ occ.remove(s.charAt(i - 1)); } while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))){ occ.add(s.charAt(rk + 1)); ++rk; } ans = Math.max(ans, rk - i + 1); } return ans; } public int lengthOfLongestSubstring1(String s) { if(s.length() <= 1) { return s.length(); } StringBuilder builder = new StringBuilder(); int max = 0; int end = 1; builder.append(s.charAt(0)); while (end < s.length()){ int num = builder.indexOf(s.charAt(end) + ""); if(num == -1){ builder.append(s.charAt(end)) ; }else { // 移动滑动窗口 builder.append(s.charAt(end)); builder.delete(0, num + 1); } max = Math.max(max, builder.length()); end++; } return max; } }
(LeetCode- 5) 最长回文子串 题目 给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
1 2 3 输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
分析 方法二:中心扩展算法 我们仔细观察一下状态转移方程:
找出其中的状态转移链
可以发现,所有的状态在转移的时候的可能性都是唯一的 。也就是说,我们可以从每一种边界情况开始「扩展」,也可以得出所有的状态对应的答案。
边界情况即为子串长度为 1 或 2 的情况。我们枚举每一种边界情况,并从对应的子串开始不断地向两边扩展。如果两边的字母相同,我们就可以继续扩展,例如从 P(i+1,j−1) 扩展到 P(i,j);如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。
聪明的读者此时应该可以发现,「边界情况」对应的子串实际上就是我们「扩展」出的回文串的「回文中心」。方法二的本质即为:我们枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值,即可得到最终的答案。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public class LongestPalindrome { public static void main(String[] args) { String s = "abcdefgfedcba"; String aa = new LongestPalindrome().longestPalindrome( s); System.out.println(""); } public String longestPalindrome(String s) { int maxStart = 0, maxEnd = 0; for(int i = 0; i < s.length(); i++){ // 以当前字母为中心,进行左右扩展 int charCenterLen = expandAroundCenter( s, i, i); int blackCenterLen = expandAroundCenter( s, i, i + 1); int len = Math.max(charCenterLen, blackCenterLen); if(len > maxEnd - maxStart){ maxStart = i - (len - 1) / 2; maxEnd = i + len / 2; } } return s.substring(maxStart, maxEnd + 1); } private int expandAroundCenter(String s, int left, int right){ while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) { left--; right++; } return right - left - 1; } }
(LeetCode-8) 字符串转换整数 (atoi) 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
注意:
1 2 本题中的空白字符只包括空格字符 `' '` 。 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "42" 输出:42 解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。 第 1 步:"42"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"42"(读入 "42") ^ 解析得到整数 42 。 由于 "42" 在范围 [-231, 231 - 1] 内,最终结果为 42 。
示例 2:
1 2 3 4 5 6 7 8 9 10 11 输入:s = " -42" 输出:-42 解释: 第 1 步:" -42"(读入前导空格,但忽视掉) ^ 第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42"(读入 "42") ^ 解析得到整数 -42 。 由于 "-42" 在范围 [-231, 231 - 1] 内,最终结果为 -42 。
示例 3:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-231, 231 - 1] 内,最终结果为 4193 。
分析 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public int myAtoi(String s) { int len = s.length(); char[] charArray = s.toCharArray(); int idx = 0; // 检查是否有空格 while (idx < len && charArray[idx] == ' '){ idx++; } // idx 和字符串的长度相等, 说明全是空格 if(idx == len){ return 0; } // 此时idx指向为第一个非空格字符,idx前面字符均可忽略 如果出现符号字符,用sign标记 int sign = 1; char firstChar = charArray[idx]; if(firstChar == '+'){ idx++; }else if(firstChar == '-') { sign = -1; idx++; } int result = 0; while (idx < len){ char currentChar = charArray[idx]; // 出现了 '0' -- '9' 之外的字符则终止 if(currentChar > '9' || currentChar < '0'){ break; } // 只能存储32位大小的有符号整数 if(result > Integer.MAX_VALUE / 10 || (result == Integer.MAX_VALUE / 10 && (currentChar - '0') > (Integer.MAX_VALUE % 10) )){ return Integer.MAX_VALUE; } if(result < Integer.MIN_VALUE / 10 || (result == Integer.MIN_VALUE / 10 && (currentChar - '0') > -(Integer.MIN_VALUE % 10) )){ return Integer.MIN_VALUE; } // 转换 result = result * 10 + sign * (currentChar - '0'); idx++; } return result; }
(LeetCode- 151) 翻转字符串里的单词 题目 给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意 :输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
1 2 输入:s = "the sky is blue" 输出:"blue is sky the"
示例 2:
1 2 3 输入:s = " hello world " 输出:"world hello" 解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
1 2 3 输入:s = "a good example" 输出:"example good a" 解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
分析 方法1 这个问题可以偷懒取巧,使用JDK为我们提供的方法来实现,比如String类中的trim()、split()方法来去除空格和分解字符串,也可以使用Collections类中的reverse方法来反转。不过性能不是特别好,而且这种解法对不起题目的难度:中等,如果面试官不允许使用上面说的方法怎么办?
其实,考察题目的示例,”the sky is blue”转换为”blue is sky the”,如果我们以单词来看,可以这样说,先读取到的单词最后出现,符合栈的定义,所以这个题目完全可以使用栈或者双端队列来实现,比如LeetCode的官方解法,时间复杂度:O(n),空间复杂度:O(n)。
方法2 除此之外,我们还可以倒着遍历原始字符串s,用空格作为单词中间的分割,每遇到空格视为读完一个单词,然后将该单词输出。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 public class ReverseWords { public static void main(String[] args) { // String s = "a good example"; // String s = " hello world "; // String s = "the sky is blue"; String s = " hello world "; String result = new ReverseWords().reverseWords(s); System.out.println(""); } public String reverseWords(String s) { char[] charArr = s.toCharArray(); int left = 0, right = s.length() - 1; // 排除字符串前后空格 while (charArr[left] == ' '){ left++; } while (charArr[right] == ' '){ right--; } StringBuilder sb = new StringBuilder(); while (left <= right){ // 倒序遍历 int index = right; while (index >= left && charArr[index] != ' '){ index--; } // 遇到单词前的空格, 取出单词,单词的范围就是index + 1 -- right for(int i = index + 1; i <= right; i++){ sb.append(charArr[i]); } if(index > left){ sb.append(' '); } // 单词之间可能有多个空格,排除 while (index >= left && charArr[index] == ' '){ index--; } // 遇见了新单词,重复开始处理 right = index; } return sb.toString(); } // public String reverseWords(String s) { // StringBuilder result = new StringBuilder(); // Stack<Character> stack = new Stack<>(); // for(int i = s.length()-1; i >= 0; i--){ // char c = s.charAt(i); // if(c == ' '){ // if(!stack.isEmpty() ){ // 单词结束 // // 清空栈 // clearnStack(result, stack); // } // }else { // stack.push(c); // } // } // // 清空栈 // clearnStack(result, stack); // return result.toString(); // } // // private void clearnStack(StringBuilder result, Stack<Character> stack) { // if(stack.isEmpty()){ // return; // } // if(result.length() == 0){ // while (!stack.isEmpty()){ // result.append(stack.pop()); // } // }else { // result.append(' '); // while (!stack.isEmpty()){ // result.append(stack.pop()); // } // } // } }
(LeetCode- 165) 比较版本号 题目 给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
如果 version1 > version2 返回 1,
如果 version1 < version2 返回 -1,
除此之外返回 0。
示例 1:
1 2 3 输入:version1 = "1.01", version2 = "1.001" 输出:0 解释:忽略前导零,"01" 和 "001" 都表示相同的整数 "1"
示例 2:
1 2 3 输入:version1 = "1.0", version2 = "1.0.0" 输出:0 解释:version1 没有指定下标为 2 的修订号,即视为 "0"
示例 3:
1 2 3 输入:version1 = "0.1", version2 = "1.1" 输出:-1 解释:version1 中下标为 0 的修订号是 "0",version2 中下标为 0 的修订号是 "1" 。0 < 1,所以 version1 < version2
分析 方法1 这个问题也使用JDK为我们提供的方法来实现。具体看代码,性能也不算低。
方法2 既然是两个字符串需要比较,我们使用两个指针i和j分别指向两个字符串的开头,然后向后遍历,当遇到小数点’.’时停下来,并将每个小数点’.’分隔开的修订号解析成数字进行比较,越靠近前边,修订号的优先级越大。根据修订号大小关系,返回相应的数值。
因此时间复杂度为 O(n + m)。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class CompareVersion { public static void main(String[] args) { String version1 = "1.01", version2 = "1.001"; int a = new CompareVersion().compareVersion( version1, version2); System.out.println(""); } public int compareVersion(String version1, String version2) { int ii = 0, j = 0; int n = version1.length(), m = version2.length(); while (ii < n || j < m){ int num1 = 0, num2 = 0; while (ii < n && version1.charAt(ii) != '.') { num1 = num1 * 10 + version1.charAt(ii++) - '0'; } while (j < m && version2.charAt(j) != '.') { num2 = num2 * 10 + version2.charAt(j++) - '0'; } if(num1 > num2 ) return 1; else if(num1 < num2) return -1; ii++;j++; } return 0; } }
(LeetCode- 76) 最小覆盖子串 题目 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
1 2 输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC"
示例 2:
1 2 输入:s = "a", t = "a" 输出:"a"
示例 3:
1 2 3 4 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
分析 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 public class MinWindow { public static void main(String[] args) { String s = "a", t = "b"; String s1 = new MinWindow().minWindow(s, t); System.out.println(""); } public String minWindow(String s, String t) { String temp = ""; Map<Character, Integer> oci = new HashMap<>(); // 滑动窗 Map<Character, Integer> oct = new HashMap<>(); // 初始化 for(int i = 0; i < t.length(); i++){ Character c = t.charAt(i); oci.put(c, oci.getOrDefault(c, 0) + 1); } int n = s.length(); int left = 0, right = 0; while (left <= right && right < n){ while (right < n && oci.get(s.charAt(right)) == null){ right++; } if(right >= n) return temp; oct.put(s.charAt(right), oct.getOrDefault(s.charAt(right), 0) + 1); // 检查是否满足条件 while (check(oci, oct)){ // 满足条件 while (oci.get(s.charAt(left)) == null){ left++; } if(temp == "" || temp.length() > right - left + 1){ temp = s.substring(left, right + 1); } oct.put(s.charAt(left), oct.getOrDefault(s.charAt(left), 0) - 1); left++; } right++; } return temp; } private boolean check(Map<Character, Integer> oci, Map<Character, Integer> oct) { for (Map.Entry<Character, Integer> entry : oci.entrySet()) { if(oct.getOrDefault(entry.getKey(), 0) < entry.getValue() ){ return false; } } return true; } public String minWindow1(String s, String t) { if (s == null || s.length() == 0 || t == null || t.length() == 0){ return ""; } /*s 和 t 由英文字母组成,所以128个够用了*/ int[] tChars = new int[128]; /*用字符串t的字符初始化字典tChars,记录每个字符出现的次数*/ for (int i = 0; i < t.length(); i++) { tChars[t.charAt(i)]++; } /*left是窗口当前左边界,right是窗口当前右边界*/ int left = 0, right = 0; /*size记录满足条件的窗口大小,count是需求的字符个数*/ int size = Integer.MAX_VALUE, count = t.length(); /*start是最小覆盖串开始的index*/ int start = 0; /*遍历所有字符*/ while (right < s.length()) { char c = s.charAt(right); if (tChars[c] > 0) {/*需要当前字符c*/ count--; } /*当前字符在tChars中的次数减一,这个次数可以为负数 * 比如当前字符在s中存在,在t中不存在 * 或者当前窗口范围内,在s中出现的次数大于t中出现的次数*/ tChars[c]--; /*窗口中已经包含所有字符*/ if (count == 0) { /*左边界向右递增,滑动窗口开始缩减,字典tChars要进行复原 * 缩减的停止处就是窗口内的字符集合刚好包含了t的全部字符,类似于示例 1中窗口包含了"BANC" * 如果字典tChars的某个字符个数小于0,说明要么当前字符在s中存在,在t中不存在 * 要么当前窗口范围内,在s中出现的次数大于t中出现的次数*/ while (left < right && tChars[s.charAt(left)] < 0) { tChars[s.charAt(left)]++; left++; } /*更新size的最小值*/ if (right - left + 1 < size) { size = right - left + 1; start = left;/*记录下最小值时候的开始位置,最后返回覆盖串时候会用到*/ } /*left向右移动后窗口肯定不能满足了重新开始循环*/ tChars[s.charAt(left)]++; left++; count++; } right++; } return size == Integer.MAX_VALUE ? "" : s.substring(start, start + size); } }