Hexo

点滴积累 豁达处之

0%

leetcode算法-位运算

Posted on In
LeetCode

leetcode算法

位运算知识补全

进制

Leetcode_92

二进制就是逢二进一，不能说你二进制比较二，规则就不一样了，基本法还是要遵守的。所以二进制里同样要遵循：1，每个位上的数字不能超过2，最大只能到1，第二，如果某个位上的数字因为运算超过了2，怎么办？往高位进位。

Leetcode_93

负数的表示

计算机中负数的表示，是以补码的形式呈现的。

原码：一个正数，按照绝对值大小转换成的二进制数；一个负数按照绝对值大小转换成的二进制数，然后最高位补1，称为原码。

比如 00000000 00000000 00000000 00000101 是 5的 原码。

10000000 00000000 00000000 00000101 是 -5的 原码。

反码：正数的反码与原码相同，负数的反码为对该数的原码除符号位外各位取反。

取反操作指：原为1，得0；原为0，得1。（1变0; 0变1）

比如：正数00000000 00000000 00000000 00000101 的反码还是 00000000 00000000 00000000 00000101

负数10000000 00000000 00000000 00000101每一位取反（除符号位），得11111111 11111111 11111111 11111010。

称：11111111 11111111 11111111 11111010 是 10000000 00000000 00000000 00000101 的反码。

补码：正数的补码与原码相同，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1.

比如：10000000 00000000 00000000 00000101 的反码是：11111111 11111111 11111111 11111010。

那么，补码为：

11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011

所以，-5 在计算机中表达为：11111111 11111111 11111111 11111011。

整数-1在计算机中如何表示。 

1
2
3
4
5
假设这也是一个int类型，那么： 
1、先取-1的原码：10000000 00000000 00000000 00000001 
2、得反码：     11111111 11111111 11111111 11111110（除符号位按位取反） 
3、得补码：     11111111 11111111 11111111 11111111 
可见，－1在计算机里用二进制表达就是全1。

负数为何在计算机中要这么表示？人类的减法运算涉及到符号位的处理，这对电路来说，是比较复杂的。补码系统下，可以通过把减法换成反码，然后通过加法器运算，这样就可以避免设计复杂的减法电路。

常用位运算

1
2
3
4
5
6
7
按位与 & (1&1=1 0&0=0 1&0=0)
按位或  |  (1|1=1 0|0=0 1|0=1)
按位非  ~(~1=0  ~0=1)
按位异或 ^ (1^1=0 1^0=1  0^0=0，很明显任何一个数和自己异或结果一定是0)
有符号右移>>(若正数,高位补0,负数,高位补1)
有符号左移<<
无符号右移>>>(不论正负,高位均补0)

常见简单面试题

取模

1
2
有趣的取模性质：取模a % (2n) 等价于 a & (2n - 1)，
所以在map里的数组个数一定是2的乘方数，计算key值在哪个元素中的时候，就用位运算来快速定位。

判断奇偶数

无需采用取模运算，只要根据数的最后一位是 0 还是 1 来决定即可，为 0 就是偶数，为 1 就是奇数。

1
2
3
if(0 == (a & 1)) {
 //偶数
}

实现数字翻倍或减半

数 a 向右移一位，相当于将 a 除以 2；数 a 向左移一位，相当于将 a 乘以 2

1
2
3
int a = 2;
a >> 1; ---> 1
a << 1; ---> 4

交换两数

位操作交换两数可以不需要第三个临时变量，虽然普通操作也可以做到，但是没有其效率高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  /*交换两数*/
  int a = 4 ,b = 6;
  int temp = a;
  a = b;
  b = temp;
  /*不借助临时变量交换两数*/
  a = a + b;
  b = a - b;
  a = a - b;
  /*位操作交换两数*/
  a=a^b;
  b=a^b;
  a=a^b;
位操作解释：
第一步：a = (a^b); 
第二步：b=a^b ---> b=(a^b)^b=a^(b^b)=a
第三步：a ^= b ---> a=(a^b)^a=(a^a)^b=b

(LeetCode-136) 只出现一次的数字

题目

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

1
2
输入: [2,2,1]
输出: 1

示例 2:

1
2
输入: [4,1,2,1,2]
输出: 4

分析

题目为什么要强调有一个数字出现一次，其他的出现两次?

我们想到了异或运算的性质:任何一个数字异或它自己都等于0。

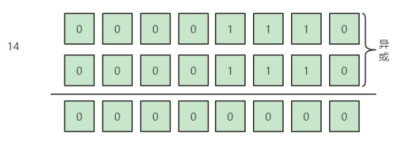
Leetcode_94

也就是说，如果我们从头到尾依次异或数组中的每一个数字，那么最终的结果刚好是那个只出现依次的数字，因为那些出现两次的数字全部在异或中抵消掉了。

代码

1
2
3
4
5
6
7
public int singleNumber(int[] nums) {
        int result = 0;
        for(int num : nums){
            result = result ^num;
        }
        return result;
    }

(**L**eetCode-**338**) 比特位计数

题目

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案

示例 1：

1
2
3
4
5
6
输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10

示例 2：

1
2
3
4
5
6
7
8
9
输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

进阶：

  • 很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
  • 你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

分析

方法1

这一题就是利用二进制位运算的经典题。本题可以利用X &= (X - 1)清除最低位的1的功能来解决。什么意思呢？

X &= (X – 1)可以清除最低位的1，利用它我们可以快速的去统计result 中1 的数量。比如：

假设X= 21，二进制表示为 0001 0101，

则 21 & 20 = 0001 0101 & 0001 0100 = 0001 0100 = 20

20&19 = 0001 0100 & 0001 0011 = 0001 0000= 16

16&15 = 0001 0000 & 0000 1111 = 0

相比原来的8次，我们这里只需3次即可知道21的二进制表示中有三个1。

对于这个题目，我们就可以反过来思考，还是以21为例，在统计21中1的个数时，其实我们只要在20的1的个数基础上加1就是21的值，而20的值又是在16的1的个数值上加1，16的值又是0的1的个数值上加1，而我们统计的次序刚好又是0,16,20,21。那就是说

N中1的个数 = N&(N-1)中1的个数+1。

想明白这一点，代码就非常简单了。

方法2

这个题目还可以利用奇偶性来解决。

对于所有的数字，只有两类：

奇数：二进制表示中，奇数一定比前面那个偶数多一个 1，因为多的就是最低位的 1。

    
1
2
3
  举例： 
0 = 0       1 = 1
2 = 10      3 = 11

偶数：二进制表示中，偶数中 1 的个数一定和除以 2 之后的那个数一样多。因为最低位是 0，除以 2 就是右移一位，也就是把那个 0 抹掉而已，所以 1 的个数是不变的。

1
2
3
举例：
2 = 10       4 = 100       8 = 1000
3 = 11       6 = 110       12 = 1100

另外，0 的 1 个数为 0，于是就可以根据奇偶性开始遍历计算了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
    public static void main(String[] args) {
        System.out.println(Arrays.toString(countBits(5)));
    }

//    public static int[] countBits(int n) {
//        int[] bits = new int[n + 1];
//        for(int i = 1; i <= n; i++){
//            bits[i] = bits[i & (i-1)] + 1;
//        }
//        return bits;
//    }

    public static int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for(int i = 1; i <= n; i++){
            bits[i] = (i & 1) == 1 ? bits[i - 1] + 1 : bits[i>>1];
        }
        return bits;
    }

(LeetCode-461) 汉明距离

题目

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

1
2
3
4
5
6
7
输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

1
2
输入：x = 3, y = 1
输出：1

分析

方法1

仔细分析题目和异或运算的中的性质：1|1=1， 0|0=0， 1|0=1，那就是说AB两数异或，将AB两数以二进制的形式表示，只有相同位置的位不同，结果数result中对应的位才是1，其余的都是0：

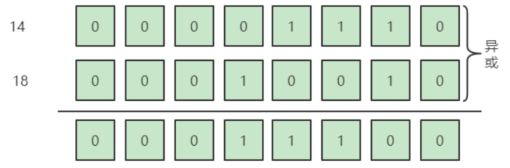
Leetcode_95

所以这个问题可以演变为两数异或后，求结果中 1 的有几个。

当然，我们可以直接利用JDK中Integer类的bitCount方法直接来求，但是这样就失去了我们刷题的初衷。

接下来我们可以这样做，可以不断地检查 result的最低位，如果最低位为1，那么令计数器加一，然后我们令result整体右移一位，这样result的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 result=0 为止。这样计数器中就累计了 result 的二进制表示中 1 的数量。

但是这么做需要循环去处理result 中的每一位，所以我们还可以借助前面所学习过的X &= (X - 1)清除最低位的1，快速的去统计result 中1 的数量。比如：

假设result = 21，二进制表示为 0001 0101，相比原来的遍历每位需要8次，我们这里只需3次即可知道21的二进制表示中有三个1。

代码

1
2
3
4
5
6
7
public int hammingDistance(int x, int y) {
      int distance = 0;
      for(int xor = x ^ y; xor != 0; xor &= (xor - 1)){
          distance++;
      }
      return distance;
  }