leetcode算法
(LeetCode-70) 爬楼梯
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
1
2
3
4
5
| 输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
|
示例 :
1
2
3
4
5
6
| 输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
|
分析
我们仔细想下,实际上,可以根据第一步的走法把所有走法分为两类,第一类是第一步走了1个台阶,另一类是第一步走了2个台阶。
所以n个台阶的走法的个数就等于先走1阶后剩下的n-1个台阶的走法个数再加上先走2阶后剩下的n-2个台阶的走法个数。用公式表示就是︰
这其实就是个递归公式,我们再来看下终止条件。当有一个台阶时,我们不需要再继续递归,就只有一种走法。所以f(1)=1。但是这个递归终止条件不够。
n=2时,f(2)=f(1)+f(0)。如果递归终止条件只有一个f(1)=1,那f(2)就无法求解了。所以除了f(⑴)=1这一个递归终止条件外,还要有f(0)=1,表示走0个台阶有一种走法,不过这样子有点滑稽。所以,我们可以把f(2)=2单独作为一种终止条件,表示走2个台阶,有两种走法,一步走完或者分两步来走。
所以,递归终止条件就是f(1)=1,f(2)=2。
综合在一起就是这样的:
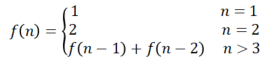
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| public class Solution {
public static void main(String[] args) {
int n = 10;
System.out.println(climbStairs(n));
System.out.println(solu2(n, 1, 2));
}
// 非递归
// public static int climbStairs(int n){
// if (n == 1) return 1;
// if (n == 2) return 2;
// int result = 0;
// int pre1 = 2;
// int pre2 = 1;
// for(int i = 3; i <= n; i++){
// result = pre1 + pre2;
// pre2 = pre1;
// pre1 = result;
//
// }
// return result;
// }
// 递归
// public static int climbStairs(int n){
// if (n == 1) return 1;
// if (n == 2) return 2;
// return climbStairs(n - 1) + climbStairs(n -2);
// }
// 递归(优化)
static Map<Integer, Integer> map = new HashMap<Integer, Integer>();
public static int climbStairs(int n){
if (n == 1) return 1;
if (n == 2) return 2;
Integer mapres = map.get(n);
if( mapres != null){
return mapres;
}
int res = climbStairs(n - 1) + climbStairs(n -2);
map.put(n, res);
return res;
}
/** 尾递归
* pre 上一步的值 2
* pre2 上上一步的值 1
* n
*/
public static int solu2(int n , int pre2, int pre){
if (n == 1) return pre2;
if (n == 2) return pre;
return solu2(n - 1, pre, pre + pre2 ) ;
}
}
|
(剑指Offer 10) 斐波那契数列
题目
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
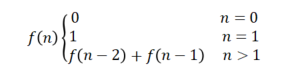
分析
可以看到,这个斐波那契数列的公式几乎和上面的“(LeetCode-70) 爬楼梯”一模一样,
代码示例 同上