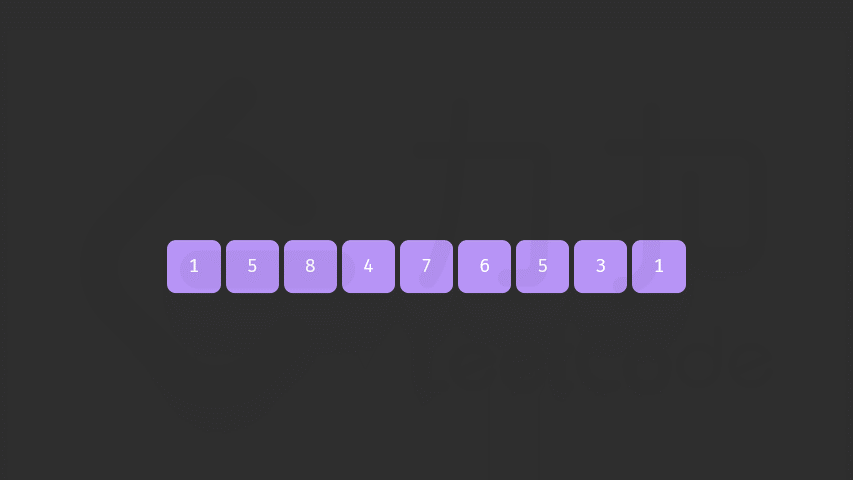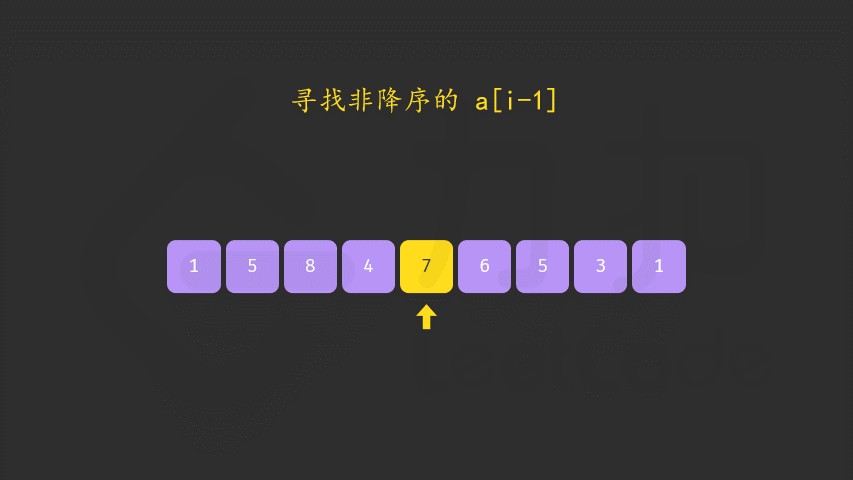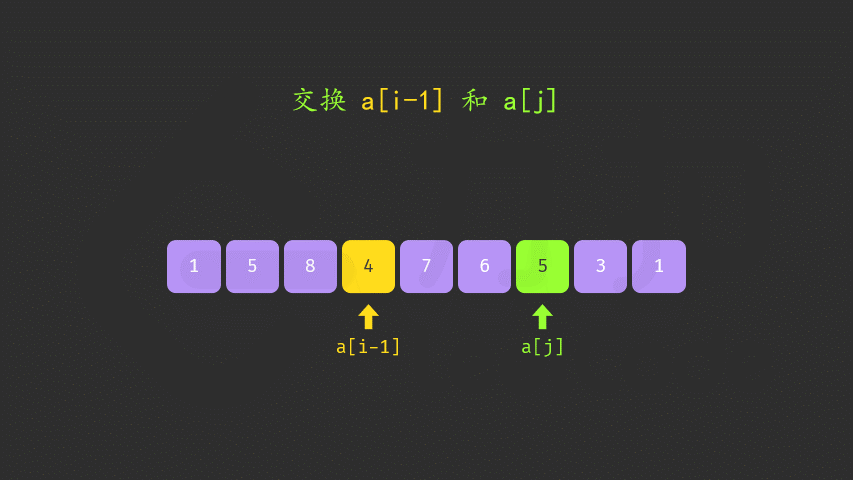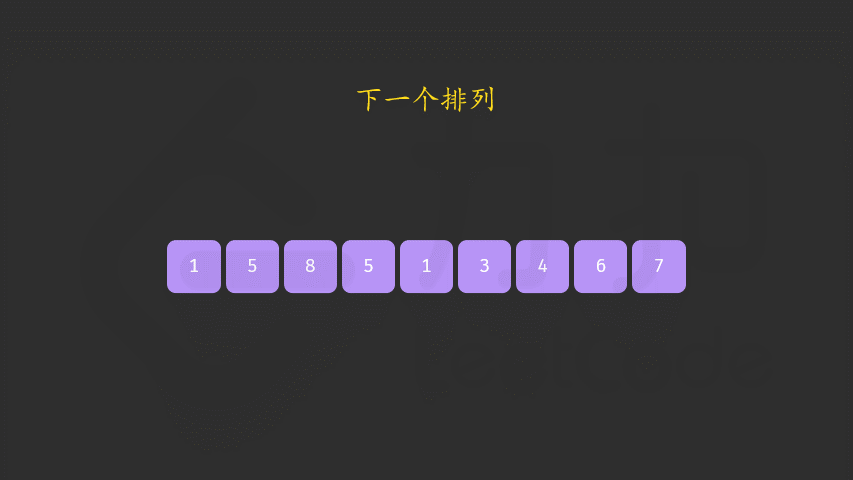leetcode算法-数组

leetcode算法

(LeetCode-1)两数之和

题目

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

1
2
3

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

1 2	输入：nums = [3,2,4], target = 6 输出：[1,2]

分析

方法1

暴力穷举，复杂度O(n2)。

对数组中每个元素，都去计算它和数组中其他元素的和sum是否等于目标值 target，如果是则返回结果，不是则继续循环，直到将所有元素检查一遍。

方法2

这道题最优的做法时间复杂度是O(n)。用一个哈希表，存储每个数对应的下标。具体做法是：顺序扫描数组，对每一个元素，在map中找能组合给定值的另一半数字，如果找到了，直接返回2个数字的下标即可。如果找不到，就把这个数字存入map 中，等待扫到“另一半”数字的时候，再取出来返回结果。

代码示例：

public class doubleSum {
    public static void main(String[] args) {
        int nums[] = {11,2,7,15};
        int target = 9;
        System.out.println(Arrays.toString(twoSum(nums, target)));
    }
    // 暴力破解
//    public static int[] twoSum(int nums[], int target){
//        for (int i = 0; i < nums.length; i++) {
//            int start = nums[i];
//            for (int j = i + 1; j < nums.length; j++) {
//                if (nums[j] + start == target){
//                    return new int[]{i,j};
//                }
//            }
//        }
//        return new int[]{};
//    }

    // 借助map
//    public static int[] twoSum(int nums[], int target){
//        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
//        for (int i = 0; i < nums.length; i++) {
//            map.put(nums[i], i);
//        }
//
//        for (int i = 0; i < nums.length; i++) {
//            Integer res = map.get(target - nums[i]);
//            if (res != null){
//                return new int[]{i,res};
//            }
//        }
//        return new int[]{};
//    }

    // 借助map(优化)
    public static int[] twoSum(int nums[], int target){
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        int [] result = new int[2];
        for (int i = 0; i < nums.length; i++) {
            int anothier = target - nums[i];
            Integer index = map.get(anothier);
            if(null != index){
                return new int[]{i,index};
            }else {
                map.put(nums[i], i);
            }
        }

        return new int[]{};
    }
}

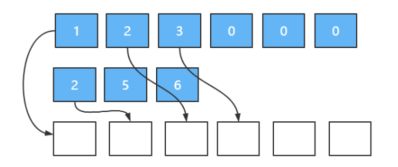
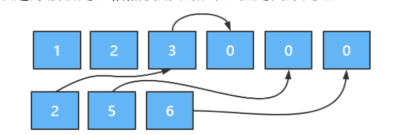
(LeetCode-88) 合并两个有序数组

题目

给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

分析

方法1

仔细观察题目我们其实可以发现，这个两个数组本身其实就是已经有序的了，这一点我们没有利用上，所以改进的办法就是利用“双指针”，每次从两个数组头部取出比较小的数字放到结果中。

这种方法的时间复杂度是多少呢？因为要把两个数组各循环一遍，所以时间复杂度是O(m+n)，在处理上因为需要一个额外的空白数组来存放两个数组的值，所以空间复杂度也是O(m+n)。

方法2

方法2中还需要一个长度为m+n的临时数组作为中转，能不能不要这个数组呢？因为题目中的整数数组 nums1的后面还有空位，完全可以利用上。所以改进方法就是，依然使用双指针，但是倒序处理。

这种情况下，时间复杂度是O(m+n)，空间复杂度则变为O(1)。

代码示例

public class DoubleArr {
    public static void main(String[] args) {
        int nums1[] = {4,5,6,0,0,0};
        int nums2[] = {1,2,3};
        merge(nums1,3, nums2,3);
        System.out.println(Arrays.toString(nums1));
    }

    // 利用jdk的api
    public static void merge(int[] nums1, int m, int[] nums2, int n) {
        for(int i = 0; i < n; i++){
            nums1[m + i] = nums1[i];
        }
        Arrays.sort(nums1);
    }

    // 双指针，从后往前遍历
//    public static void merge(int[] nums1, int m, int[] nums2, int n) {
//        int index1 = m - 1;  // 数组一的最大下标(不包含末尾非有效数字)
//        int index2 = n - 1;   // 数组二的最大下标
//        int resultIndex = m + n - 1;  // 数组一的最大下标(包含末尾非有效数字)
//
//        while (index1 >= 0 && index2 >= 0){
//            int num1 = nums1[index1];
//            int num2 = nums2[index2];
//            if (num1 > num2){
//                index1--;
//                nums1[resultIndex] = num1;
//            }else {
//                nums1[resultIndex] = num2;
//                index2--;
//            }
//            resultIndex--;
//        }
//
//        if (index2 >= 0){ // 数组2 还有剩余  同步移动
//            for (int i = 0; i <= index2; i++) {
//                nums1[i] = nums2[i];
//            }
//        }
//    }
}

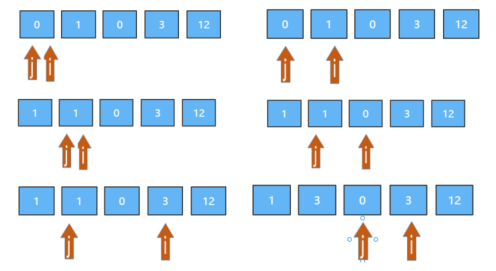
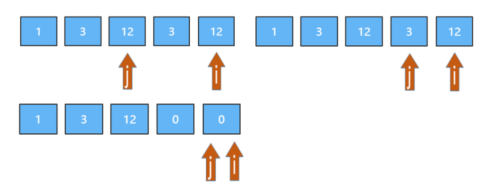
(LeetCode-283)移动零

题目

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

1 2	输入: [0,1,0,3,12] 输出: [1,3,12,0,0]

说明:

必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数

分析

方法

依然可以用双指针的办法，两个指针i和j。i负责遍历整个数组，在遍历数组的时候，j用来记录当前所有非0元素的个数。遍历的时候每遇到一个非0元素就将其往数组左边挪，挪动到J所在的位置，注意是挪动，不是交换位置，j同时也移动一个位置。当第一次遍历完后，j指针的下标就指向了已经排完了位置的最后一个非0元素下标。

进行第二次遍历的时候，起始位置就从j开始到结束，将剩下的这段区域内的元素全部置为0即可。

代码示例

public class MoveZero {
    public static void main(String[] args) {
      //  int nums[] = {0,1,0,3,12};
      //  int nums[] = {0,0,0,3,12};
        int nums[] = {0,12,0,3,0};
        moveZeroes(nums);
        System.out.println(Arrays.toString(nums));
    }

    // 交换(一次遍历)
//    public static void moveZeroes(int[] nums) {
//        int iz = 0; // 需移动的起始位置
//        int moveNum = 0; // 0的个数
//        for(int i = 0; i < nums.length; i++){
//            if(nums[i] == 0){
//                moveNum+=1;
//            }
//            if( nums[i] != 0){
//               if (moveNum > 0){  // 移动
//                   nums[iz] = nums[i];
//                   nums[i] = 0;
//               }
//                iz+=1;
//            }
//        }
//    }

    // 整体清除(两次遍历)
    public static void moveZeroes(int[] nums) {
        int j = 0; // 需移动的起始位置
        for(int i = 0; i < nums.length; i++){
            if(nums[i] != 0){
                nums[j++] = nums[i];
            }
        }

        for(int i = j; i < nums.length; i++){
            nums[j++] = 0;
        }
    }
}

(LeetCode-448)找到所有数组中消失的数字

题目

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例 1：

1 2	输入：nums = [4,3,2,7,8,2,3,1] 输出：[5,6]

示例 2：

1 2	输入：nums = [1,1] 输出：[2]

提示：

1
2
3

n == nums.length
1 <= n <= 105
1 <= nums[i] <= n

进阶：你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。

public class DailNum {
    public static void main(String[] args) {
        int nums[] = {4,3,2,7,8,2,3,1};
        for(Integer aa : findDisappearedNumbers(nums)){
            System.out.println(aa);
        }
    }
    public static List<Integer> findDisappearedNumbers(int[] nums) {
        int n = nums.length;
        for(int num : nums){
            int x = (num - 1) % n;  // 对n 取模来还原它本来的值
            nums[x] += n;
        }
        List<Integer> result = new ArrayList<Integer>();
        for(int i = 0; i < n; i++){
            if(nums[i] <= n){
                result.add(i + 1);
            }
        }
        return result;

    }
}

(LeetCode-169) 多数元素

题目

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

1 2	输入：nums = [3,2,3] 输出：3

示例 2：

1 2	输入：nums = [2,2,1,1,1,2,2] 输出：2

分析

方法1

很明显，这个题可以使用HashMap来解决这个问题，key表示一个元素，value表示该元素出现的次数。

我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。

很明显这种方法的时间复杂度就是O(n)，空间复杂度也是O(n)，但是不符合题目进阶的要求，所以我们不考虑具体的实现。

方法2

这个问题还可以使用Boyer-Moore 投票算法来解决。

这个算法是个什么意思呢？它的核心思想就是对拼消耗。

比如玩一个诸侯争霸的游戏，游戏的胜利条件是：最后还有人活下来的国家就是赢家。

假设你的人口超过总人口一半以上，而且你微操也不错，能保证每个人口出去干仗都能一对一同归于尽。那就完全可以大混战，即使最差的情况下所有人都联合起来对付你，最后肯定你赢。把其他的国家的所有人全部一对一兑子，最后能剩下的必定是自己人。

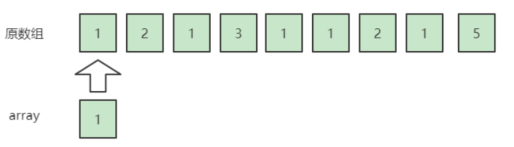
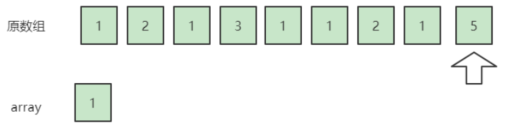
用个实例来看看，我们引入一个array数组。

为了方便理解举一个示例输入：{1,2,1,3,1,1,2,1,5}

从第一个数字1开始，我们想要把它和一个不是1的数字一起从数组里抵消掉，但是目前我们只扫描了一个1，所以暂时无法抵消它，把它加入到array，array变成了{1}。

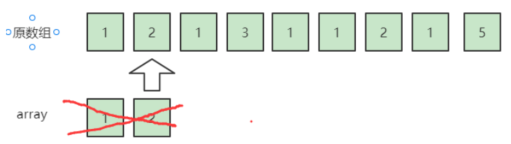
然后继续扫描第二个数，是2，我们可以把它和一个不是2的数字抵消掉了，因为我们之前扫描到一个1，所以array变成了{}。

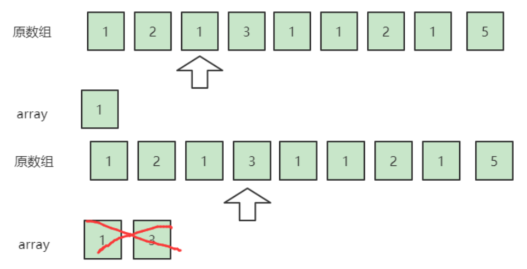
继续扫描第三个数1，无法抵消，于是array变成了{1}；接下来扫描到3,可以将3和array数组里面的1抵消,于是array变成了{}。

接下来扫描到1，此时array为空，所以无法抵消这个1，array变成了{1}；接下来扫描到1，此时虽然array不为空，但是array里也是1，所以还是无法抵消，把它也加入这个array,于是array变成了{1,1}（其实到这我们可以发现，array里面只可能同时存在一种数，因为只有array为空或当前扫描到的数和array里的数字相同时才把这个数字放入array）。

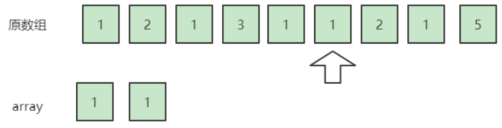
接下来扫描到2，把它和一个1抵消掉，至于抵消哪一个1，无所谓，array变成了{1}。

接下来扫描到1，不能抵消，array变成了{1,1}，result{1,1,5}接下来扫描到5，可以将5和一个1抵消，array变成了{1}

至此扫描完成了数组里的所有数，array里剩了1，所以1就是大于一半的数字。

再回顾一下这个过程，其实就是删除（抵消）了（1，2），（1，3），（1，5）剩下了一个1。

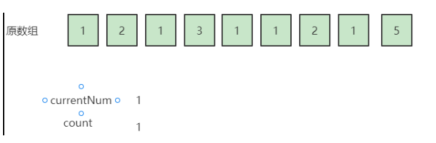
可以看到，前面提到array里只可能同时存储一种数字，所以我们用两个变量来优化上述过程，currentNum来表示当前array里存储的数，count表示array的长度，即目前暂时无法删除的元素个数。

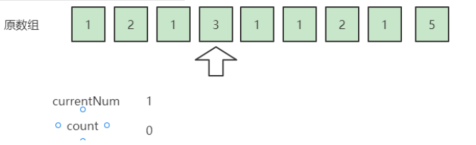
依然输入为：{1,2,1,3,1,1,2,1,5}，用这两个变量再重复一遍上面的过程，currentNum 初始化为数组第一个元素，count 初始化为1

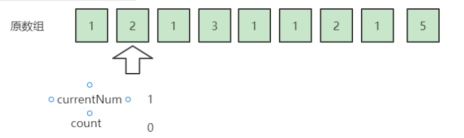
扫描到2，它不等于currentNum，于是可以抵消掉一个currentNum， count -= 1，此时count = 0,其实可以理解为扫到的元素都抵消完了，这里可以暂时不改变currentNum的值。

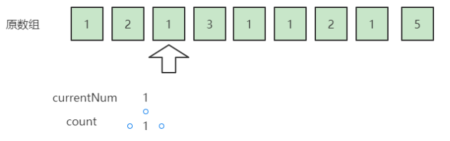
扫描到1，它等于currentNum，于是count += 1 => count = 1

扫描到3，它不等于currentNum，可以抵消一个currentNum => count -= 1 => count = 0，此时又抵消完了。

扫描到1，它等于currentNum，于是count += 1 => count = 1

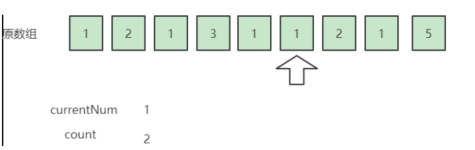
扫描到1，他等于currentNum，无法抵消 => count += 1 => count = 2 (扫描完前六个数，剩两个1无法抵消)

扫描到2，它不等于currentNum，可以抵消一个currentNum => count -= 1 => count = 1,此时还剩1个1没有被抵消

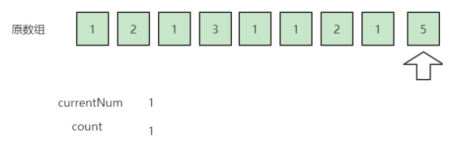
扫描到1，它等于currentNum，无法抵消 => count += 1 => count = 2

扫描到5，它不等于currentNum，可以抵消一个currentNum => count -= 1 => count = 1至此扫描完成，还剩1个1没有被抵消掉，它就是我们要找的数。

(LeetCode-11) 盛最多水的容器

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

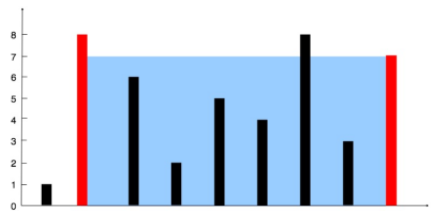
1
2
3

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

1 2	输入：height = [1,1] 输出：1

分析

方法一：双指针

我们先从题目中的示例开始，一步一步地解释双指针算法的过程。稍后再给出算法正确性的证明。

题目中的示例为：

1 2	[1, 8, 6, 2, 5, 4, 8, 3, 7] ^ ^

在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \min(1, 7) * 8 = 8min(1,7)∗8=8。

此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由

1	两个指针指向的数字中较小值∗指针之间的距离

决定的。如果我们移动数字较大的那个指针，那么前者「两个指针指向的数字中较小值」不会增加，后者「指针之间的距离」会减小，那么这个乘积会减小。因此，我们移动数字较大的那个指针是不合理的。因此，我们移动数字较小的那个指针。

所以，我们将左指针向右移动：

1 2	[1, 8, 6, 2, 5, 4, 8, 3, 7] ^ ^

此时可以容纳的水量为 \min(8, 7) * 7 = 49min(8,7)∗7=49。由于右指针对应的数字较小，我们移动右指针：

1 2	[1, 8, 6, 2, 5, 4, 8, 3, 7] ^ ^

此时可以容纳的水量为 min(8, 3) * 6 = 18min(8,3)∗6=18。由于右指针对应的数字较小，我们移动右指针：

1 2	[1, 8, 6, 2, 5, 4, 8, 3, 7] ^ ^

此时可以容纳的水量为 min(8, 8) * 5 = 40min(8,8)∗5=40。两指针对应的数字相同，我们可以任意移动一个，例如左指针：

1 2	[1, 8, 6, 2, 5, 4, 8, 3, 7] ^ ^

此时可以容纳的水量为 min(6, 8) * 4 = 24min(6,8)∗4=24。由于左指针对应的数字较小，我们移动左指针，并且可以发现，在这之后左指针对应的数字总是较小，因此我们会一直移动左指针，直到两个指针重合。在这期间，对应的可以容纳的水量为：min(2, 8) * 3 = 6min(2,8)∗3=6，min(5, 8) * 2 = 10min(5,8)∗2=10，min(4, 8) * 1 = 4min(4,8)∗1=4。

在我们移动指针的过程中，计算到的最多可以容纳的数量为 4949，即为最终的答案。

代码

public class MaxArea {

    public static void main(String[] args) {
        int[] nums = {1,8,6,2,5,4,8,3,7};
        System.out.println(maxArea(nums));
    }

    public static int maxArea(int[] height) {
        int i = 0, j = height.length - 1;
        int masWater = 0;
        while(i < j){
            if(height[i] < height[j]){
                masWater = Math.max(masWater, (j - i ) * height[i++]);
            }else {
                masWater = Math.max(masWater, (j - i ) * height[j--]);
            }

        }
        return masWater;
    }
}

(LeetCode-15) 三数之和

题目

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

1
2
3

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

1
2
3

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

分析

解题思路：

暴力法搜索为 O(N^3)时间复杂度，可通过双指针动态消去无效解来优化效率。
双指针法铺垫：先将给定 nums 排序，复杂度为 O(NlogN)。
双指针法思路：固定 3 个指针中最左（最小）数字的指针 k，双指针 i，j 分设在数组索引 (k, len(nums))两端，通过双指针交替向中间移动，记录对于每个固定指针 k 的所有满足 nums[k] + nums[i] + nums[j] == 0 的 i,j 组合：
- 当 nums[k] > 0 时直接break跳出：因为 nums[j] >= nums[i] >= nums[k] > 0，即 33 个数字都大于 00 ，在此固定指针 k 之后不可能再找到结果了。
- 当 k > 0且nums[k] == nums[k - 1]时即跳过此元素nums[k]：因为已经将 nums[k - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。
- i，j 分设在数组索引 (k, len(nums))两端，当i < j时循环计算s = nums[k] + nums[i] + nums[j]，并按照以下规则执行双指针移动：
  当s < 0时，i += 1并跳过所有重复的nums[i]；
  当s > 0时，j -= 1并跳过所有重复的nums[j]；
  当s == 0时，记录组合[k, i, j]至res，执行i += 1和j -= 1并跳过所有重复的nums[i]和nums[j]，防止记录到重复组合。

代码

public class ThreeSum {

    public static void main(String[] args) {
        int[] nums = {-1,0,1,2,-1,-4};
        List<List<Integer>> list = threeSum(nums);
        System.out.println("");
    }

    public static List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        for(int k = 0; k < nums.length - 2; k++){
            if(nums[k] > 0) break;
            if(k > 0 && nums[k] == nums[k - 1]) continue;
            int i = k + 1, j = nums.length - 1;
            while(i < j){
                int sum = nums[k] + nums[i] + nums[j];
                if(sum < 0){
                    while(i < j && nums[i] == nums[++i]); // 数字重复，则结果还是小于0，继续查找下一个
                } else if (sum > 0) {
                    while(i < j && nums[j] == nums[--j]);
                } else {
                    res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[i], nums[j])));
                    while(i < j && nums[i] == nums[++i]);
                    while(i < j && nums[j] == nums[--j]);
                }
            }
        }
        return res;
    }
}

(LeetCode-31)下一个排列

题目

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]

整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的下一个排列就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

示例 1：

1 2	输入：nums = [1,2,3] 输出：[1,3,2]

示例 2：

1 2	输入：nums = [3,2,1] 输出：[1,2,3]

示例 3：

1 2	输入：nums = [1,1,5] 输出：[1,5,1]

分析

方法一：两遍扫描

思路及解法

注意到下一个排列总是比当前排列要大，除非该排列已经是最大的排列。我们希望找到一种方法，能够找到一个大于当前序列的新序列，且变大的幅度尽可能小。具体地：

我们需要将一个左边的「较小数」与一个右边的「较大数」交换，以能够让当前排列变大，从而得到下一个排列。
同时我们要让这个「较小数」尽量靠右，而「较大数」尽可能小。当交换完成后，「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下，使变大的幅度尽可能小。

以排列 [4,5,2,6,3,1][4,5,2,6,3,1] 为例：

我们能找到的符合条件的一对「较小数」与「较大数」的组合为 2 与 3，满足「较小数」尽量靠右，而「较大数」尽可能小。
当我们完成交换后排列变为 [4,5,3,6,2,1][4,5,3,6,2,1]，此时我们可以重排「较小数」右边的序列，序列变为 [4,5,3,1,2,6][4,5,3,1,2,6]。

具体地，我们这样描述该算法，对于长度为 n 的排列 a：

首先从后向前查找第一个顺序对 (i,i+1)，满足 a[i] < a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。

如果找到了顺序对，那么在区间[i+1,n) 中从后向前查找第一个元素 jj 满足 a[i] < a[j]。这样「较大数」即为 a[j]。

交换 a[i] 与 a[j，此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n)使其变为升序，而无需对该区间进行排序。

注意

如果在步骤 1 找不到顺序对，说明当前序列已经是一个降序序列，即最大的序列，我们直接跳过步骤 2 执行步骤 3，即可得到最小的升序序列。

代码

public class NextPermutation {
    public static void main(String[] args) {
        int[] nums = {1,2};
        nextPermutation(nums);
        System.out.println(Arrays.toString(nums));
    }

    public static void nextPermutation(int[] nums) {
        int numCount = nums.length;
        int start = numCount - 2;
        while (start >= 0 && nums[start] >= nums[start + 1]) {  // 寻找 较小数
            start = start -1;
        }

        if(start >= 0){
            int end = nums.length - 1;
            while (end >= 0 && nums[start] >= nums[end]){  // 寻找较大值
                end = end - 1;
            }
            swap( nums, start, end);
        }
        reverse( nums,  start + 1);
    }
    public static  void reverse(int[] nums, int start) {
       int left = start, right = nums.length - 1;
       while(left < right){
           swap(nums, left, right);
           left++;
           right--;
       }
    }
    public static  void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

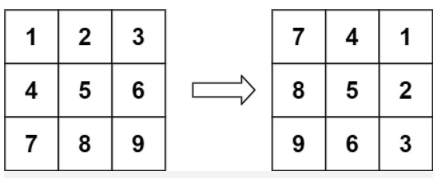
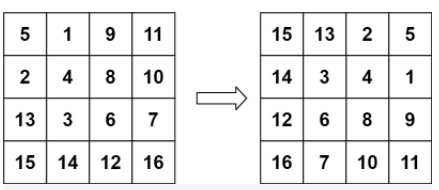
(LeetCode-48) 旋转图像

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1：

1 2	输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

1 2	输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

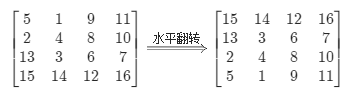
分析

方法：用翻转代替旋转

我们以题目中的示例

作为例子，先将其通过水平轴翻转得到：

再根据主对角线翻转得到：

就得到了答案。这是为什么呢？对于水平轴翻转而言，我们只需要枚举矩阵上半部分的元素，和下半部分的元素进行交换，即

对于主对角线翻转而言，我们只需要枚举对角线左侧的元素，和右侧的元素进行交换，即

代码

public class Rotate {
    public static void main(String[] args) {
        int[][] matrix = {{5,1,9,11},{2,4,8,10},{13,3,6,7},{15,14,12,16}};
        rotate( matrix);
        System.out.println("");
    }
    public static void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < n; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        // 主对角线翻转
        for(int i = 0; i < n ; i++){
            for(int j = 0; j <= i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

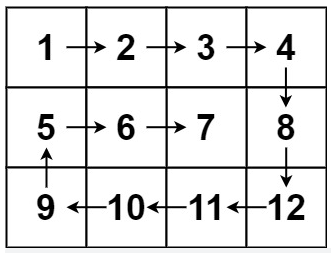
(LeetCode-54) 螺旋矩阵

题目

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

1 2	输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5]

示例 2：

1 2	输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

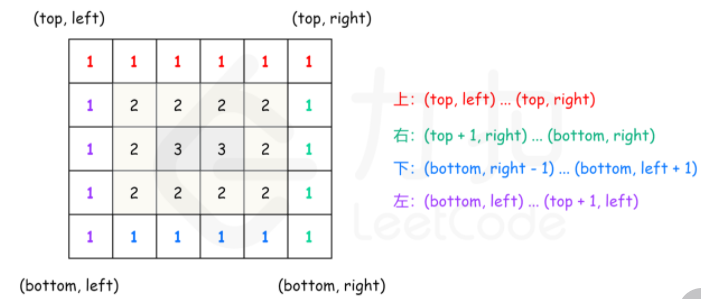
分析

方法二：按层模拟

可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。

定义矩阵的第 kk 层是到最近边界距离为 kk 的所有顶点。例如，下图矩阵最外层元素都是第 1 层，次外层元素都是第 2 层，剩下的元素都是第 3 层。

[[1, 1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1, 1]]

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于(top,left)，右下角位于 (bottom,right)，按照如下顺序遍历当前层的元素。

从左到右遍历上侧元素，依次为(top,left) 到(top,right)。
从上到下遍历右侧元素，依次为 (top+1,right) 到 (bottom,right)。
如果left<right 且 top<bottom，则从右到左遍历下侧元素，依次为(bottom,right−1) 到(bottom,left+1)，以及从下到上遍历左侧元素，依次为 (bottom,left) 到(top+1,left)。

遍历完当前层的元素之后，将 left 和 top 分别增加 11，将 right 和bottom 分别减少 11，进入下一层继续遍历，直到遍历完所有元素为止。

代码

public class SpiralOrder {

    public static void main(String[] args) {
       // int[][] matrix = {{1, 2,3},{4,5,6},{7,8,9}};
        int[][] matrix = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};
        //[[1,2,3,4],[5,6,7,8],[9,10,11,12]]
        List<Integer> list = spiralOrder( matrix);
        System.out.println("");
    }

    public static  List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        // 边界判断
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        // 行 列
        int rows = matrix.length, columns = matrix[0].length;
        // 边界值
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        // 遍历 边界值为截止条件
        while (left <= right && top <= bottom) {
            // 左  ->  右
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            // 上 -- >  下
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            // 如果左等于又，或上等于下 则说明为单列或单行，则无需反向操作
            if (left < right && top < bottom) {
                // 右  -> 左
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                // 下 -- >  上
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            // 当前层遍历完， 缩小边界值
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

(LeetCode-55) 跳跃游戏

题目

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

1
2
3

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

1
2
3

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

分析

方法1

这个问题，一定要看清楚题目中的“最大长度”，也就是说，如果某个元素的值为3，能够跳跃的长度有1,2,3这三种选择，并不是只能跳跃3步。

由此我们可以推出，如果数组中的元素没有为0的，比如全部都是1或者是大于1的数，那就一定可以到达数组的末尾。如果数组中的元素存在0，则必须在0值之前找到一个值，能够避开这个0，否则的话是没法到达数组的末尾。

于是，这个题目就可以这样处理了：从后往前遍历，如果遇到nums[i] = 0，就找i前面的元素j，使得nums[j] > i - j。如果找不到，则不可能跳跃到num[i+1]，只会落在nums[i] = 0上，返回false。

虽然在具体的代码实现上会有两个循环，但是实际值遍历了数组一次，所以时间复杂度就是O(n)。

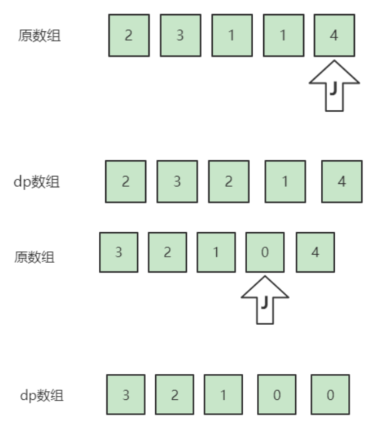
方法2

这个问题，还可以用动态规划来求解，这是个非常明显的“多阶段决策最优解”类型的问题，每达到一个数组的元素，都是一个决策，这个决策的最优解就是我们当前阶段我们能够跳跃的最大值是多少。

很明显，按照我们求解动态规划问题的步骤和思想，首先设定一个dp数组，dp[i]表示在下标i处能够跳跃的最大值。

对于dp[i]，它等于dp[i-1]跳一格到达i处后剩余的步数和nums[i]的两者中的最大值。因此状态转移方程为：dp[i]=max(dp[i-1]-1,nums[i])

初始化条件就是dp[0]=nums[0]。

在每次循环开始，我们判断dp[i-1]是否等于0，若是，则不可能到达下标i处，因此直接返回false。循环结束后返回true。

不过仔细分析上述过程可以发现，dp[i]只和dp[i-1]有关，因此可以用一个变量来取代数组。

代码

public class CanJump {
    public static void main(String[] args) {
       int[] nums = {3,2,1,0,4};
       // int[] nums = {2,3,1,1,4};
        System.out.println(canJump( nums));
    }

    // 动态规划
    public static boolean canJump(int[] nums) {
        int n = nums.length;
        int maxStep = nums[0];
        for(int i = 1; i < n; i++){
            if(maxStep == 0) return false;
            maxStep = Math.max(nums[i], maxStep - 1);
        }
        return true;
    }

    // 遍历查找为0的是否可以跳过
//    public static boolean canJump(int[] nums) {
//        if(nums == null || nums.length < 2){
//            return true;
//        }
//        for(int i = nums.length - 2; i >= 0; i--){
//            if(nums[i] == 0){
//                if(!checkJump(nums, i)){
//                    return false;
//                }
//            }
//        }
//        return true;
//    }
//
//    // 是否可以调过
//    private static boolean checkJump(int[] nums, int i) {
//        int index = i - 1 ;
//        while(index >= 0 ){
//            if(nums[index] > i - index ){
//                return true;
//            }
//            index--;
//        }
//        return false;
//    }
}

(LeetCode-215)数组中的第K个最大元素

题目

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

1 2	输入: [3,2,1,5,6,4], k = 2 输出: 5

示例 2:

1 2	输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4

分析

方法一：基于快速排序的选择方法

思路和算法

我们可以用快速排序来解决这个问题，先对原数组排序，再返回倒数第 kk 个位置，这样平均时间复杂度是O(nlogn)，但其实我们可以做的更快。

首先我们来回顾一下快速排序，这是一个典型的分治算法。我们对数组a[l⋯r] 做快速排序的过程是（参考《算法导论》）：

分解：将数组 a[l⋯r] 「划分」成两个子数组 a[l⋯q−1]、a[q+1⋯r]，使得 a[l⋯q−1] 中的每个元素小于等于 a[q]，且 a[q] 小于等于 a[q+1⋯r] 中的每个元素。其中，计算下标 q 也是「划分」过程的一部分。
解决：通过递归调用快速排序，对子数组 a[l⋯q−1] 和 a[q+1⋯r] 进行排序。
合并：因为子数组都是原址排序的，所以不需要进行合并操作，a[l⋯r] 已经有序。
上文中提到的「划分」过程是：从子数组 a[l⋯r] 中选择任意一个元素 x 作为主元，调整子数组的元素使得左边的元素都小于等于它，右边的元素都大于等于它， xx 的最终位置就是 q。

由此可以发现每次经过「划分」操作后，我们一定可以确定一个元素的最终位置，即 x 的最终位置为 q，并且保证 a[l⋯q−1] 中的每个元素小于等于a[q]，且 a[q] 小于等于 a[q+1⋯r] 中的每个元素。所以只要某次划分的 q 为倒数第 k 个下标的时候，我们就已经找到了答案。我们只关心这一点，至于 a[l⋯q−1] 和 a[q+1⋯r] 是否是有序的，我们不关心。

代码

public class QuickSort {

    public static void main(String[] args) {
        int[] nums = {3,2,1,5,6,4};
        int temp = findKthLargest( nums, 2);
        System.out.println(temp);
     }

     public static int findKthLargest(int[] nums, int k){
         int baseNum = nums[0];
         int start = 0;
         int end = nums.length - 1;
         // 转化一下， 第k个元素的下标是nums.length  - k
         int target = nums.length  - k;
         while(true){
             int temp = partition( nums,  start,  end);
             if(temp == target){
                 return nums[temp];
             }else if(temp < target){
                 start = temp + 1;
             }else{
                 end = temp - 1;
             }
         }
     }

//    public static int partition(int[] nums, int start, int end){
//        int i = start;
//        int j = end;
//        if(i == j) return i;
//        int baseNum = nums[i];
//        if(i < j){
//            //
//            while (i < j){
//                while (i < j && baseNum < nums[j]) {
//                    j--;
//                }
//                if(i < j) {
//                    nums[i] = nums[j];
//                    i++;
//                }
//                while (i < j && baseNum > nums[i]){
//                    i++;
//                }
//                if(i < j) {
//                    nums[j] = nums[i];
//                    j--;
//                }
//            }
//            nums[i] = baseNum;
//        }
//        int result = i;
//        return result ;
//    }

    /**
     * 快速排序分区方法
     */
    public static int partition(int[] array, int start, int end) {
        /*只有一个元素时，无需再分区*/
        if(start == end) return start;
        /*随机选取一个基准数*/
        int pivot = start;
        /*zoneIndex是分区指示器，初始值为分区头元素下标减一*/
        int zoneIndex = start - 1;
        /*将基准数和分区尾元素交换位置*/
        swap(array, pivot, end);
        for (int i = start; i <= end; i++){
            /*当前元素小于等于基准数*/
            if (array[i] <= array[end]) {
                /*首先分区指示器累加*/
                zoneIndex++;
                /*当前元素在分区指示器的右边时，交换当前元素和分区指示器元素*/
                if (i > zoneIndex)
                    swap(array, i, zoneIndex);
            }
        }
        return zoneIndex;
    }

    /**
     * 交换数组内两个元素
     */
    public static void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
}

(LeetCode-347) 前 K 个高频元素

题目

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

1 2	输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]

示例 2:

1 2	输入: nums = [1], k = 1 输出: [1]

分析

方法一：堆

思路与算法

首先遍历整个数组，并使用哈希表记录每个数字出现的次数，并形成一个「出现次数数组」。找出原数组的前 kk 个高频元素，就相当于找出「出现次数数组」的前 kk 大的值。

最简单的做法是给「出现次数数组」排序。但由于可能有O(N) 个不同的出现次数（其中 N 为原数组长度），故总的算法复杂度会达到 O(NlogN)，不满足题目的要求。

在这里，我们可以利用堆的思想：建立一个小顶堆，然后遍历「出现次数数组」：

如果堆的元素个数小于 k，就可以直接插入堆中。
如果堆的元素个数等于 k，则检查堆顶与当前出现次数的大小。如果堆顶更大，说明至少有 k 个数字的出现次数比当前值大，故舍弃当前值；否则，就弹出堆顶，并将当前值插入堆中。

遍历完成后，堆中的元素就代表了「出现次数数组」中前 k 大的值。

代码

public class TopKFrequent {

    public static void main(String[] args) {
        int[] nums = {1,1,1,2,2,2,2,4,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,6,6,3};
        int[] result = topKFrequent( nums,  2);
        System.out.println(Arrays.toString(result));
    }

    public static int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> occurrences = new HashMap<Integer, Integer>();
        for (int num : nums) {
            occurrences.put(num, occurrences.getOrDefault(num, 0) + 1);
        }

        // int[] 的第一个元素代表数组的值，第二个元素代表了该值出现的次数
        PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] m, int[] n) {
                return m[1] - n[1];
            }
        });
        for (Map.Entry<Integer, Integer> entry : occurrences.entrySet()) {
            int num = entry.getKey(), count = entry.getValue();
            if (queue.size() == k) {
                if (queue.peek()[1] < count) {
                    queue.poll();
                    queue.offer(new int[]{num, count});
                }
            } else {
                queue.offer(new int[]{num, count});
            }
        }
        int[] ret = new int[k];
        for (int i = 0; i < k; ++i) {
            ret[i] = queue.poll()[0];
        }
        return ret;
    }
}

(LeetCode-4) 寻找两个正序数组的中位数

题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

1
2
3

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

1
2
3

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

分析

方法一：二分查找

给定两个有序数组，要求找到两个有序数组的中位数，最直观的思路有以下两种：

使用归并的方式，合并两个有序数组，得到一个大的有序数组。大的有序数组的中间位置的元素，即为中位数。
不需要合并两个有序数组，只要找到中位数的位置即可。由于两个数组的长度已知，因此中位数对应的两个数组的下标之和也是已知的。维护两个指针，初始时分别指向两个数组的下标 0 的位置，每次将指向较小值的指针后移一位（如果一个指针已经到达数组末尾，则只需要移动另一个数组的指针），直到到达中位数的位置。

假设两个有序数组的长度分别为 m 和 n，上述两种思路的复杂度如何？

第一种思路的时间复杂度是 O(m+n)，空间复杂度是 O(m+n)。第二种思路虽然可以将空间复杂度降到 O(1)，但是时间复杂度仍是 O(m+n)。

如何把时间复杂度降低到 O(log(m+n)) 呢？如果对时间复杂度的要求有 log，通常都需要用到二分查找，这道题也可以通过二分查找实现。

根据中位数的定义，当 m+n 是奇数时，中位数是两个有序数组中的第(m+n)/2 个元素，当m+n 是偶数时，中位数是两个有序数组中的第(m+n)/2 个元素和第(m+n)/2+1 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为(m+n)/2 或(m+n)/2+1。

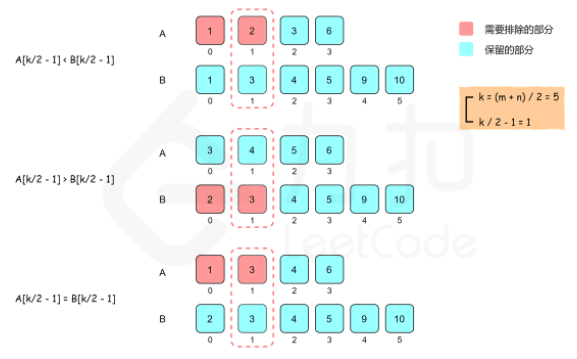
假设两个有序数组分别是 A 和 B。要找到第 k 个元素，我们可以比较 A[k/2−1] 和 B[k/2−1]，其中 / 表示整数除法。由于 A[k/2−1] 和 B[k/2−1] 的前面分别有 A[0..k/2−2] 和 B[0..k/2−2]，即 k/2−1 个元素，对于A[k/2−1] 和 B[k/2−1] 中的较小值，最多只会有 (k/2−1)+(k/2−1)≤k−2 个元素比它小，那么它就不能是第 kk 小的数了。

因此我们可以归纳出三种情况：

如果 [k/2-1] < B[k/2−1]，则比 A[k/2−1] 小的数最多只有 A 的前 k/2−1 个数和 B 的前 k/2−1 个数，即比 A[k/2−1] 小的数最多只有k−2 个，因此 A[k/2−1] 不可能是第 kk 个数，A[0] 到 A[k/2−1] 也都不可能是第 k 个数，可以全部排除。
如果 A[k/2−1] > B[k/2−1]，则可以排除 B[0] 到 B[k/2−1]。
如果 A[k/2−1] = B[k/2−1]，则可以归入第一种情况处理。

可以看到，比较 A[k/2−1] 和 B[k/2−1] 之后，可以排除 k/2 个不可能是第 k 小的数，查找范围缩小了一半。同时，我们将在排除后的新数组上继续进行二分查找，并且根据我们排除数的个数，减少 k 的值，这是因为我们排除的数都不大于第 k 小的数。

有以下三种情况需要特殊处理：

如果 A[k/2−1] 或者 B[k/2−1] 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 k 的值，而不能直接将 k 减去k/2。
如果一个数组为空，说明该数组中的所有元素都被排除，我们可以直接返回另一个数组中第 k 小的元素。
如果 k=1，我们只要返回两个数组首元素的最小值即可。

用一个例子说明上述算法。假设两个有序数组如下：

1 2	A: 1 3 4 9 B: 1 2 3 4 5 6 7 8 9

两个有序数组的长度分别是 4 和 9，长度之和是 13，中位数是两个有序数组中的第 7 个元素，因此需要找到第 k=7 个元素。

比较两个有序数组中下标为 k/2−1=2 的数，即A[2] 和B[2]，如下面所示：

A: 1 3 4 9
       ↑
B: 1 2 3 4 5 6 7 8 9
       ↑

由于A[2]>B[2]，因此排除 B[0] 到 B[2]，即数组 B 的下标偏移（offset）变为 3，同时更新 k 的值：k=k−k/2=4。

下一步寻找，比较两个有序数组中下标为 k/2−1=1 的数，即 A[1] 和 B[4]，如下面所示，其中方括号部分表示已经被排除的数。

A: 1 3 4 9
     ↑
B: [1 2 3] 4 5 6 7 8 9
             ↑

由于 A[1]<B[4]，因此排除A[0] 到 A[1]，即数组 A 的下标偏移变为 2，同时更新 k 的值：k=k−k/2=2。

下一步寻找，比较两个有序数组中下标为k/2−1=0 的数，即比较A[2] 和 B[3]，如下面所示，其中方括号部分表示已经被排除的数。

A: [1 3] 4 9
         ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

由于A[2]=B[3]，根据之前的规则，排除A 中的元素，因此排除 A[2]，即数组 A 的下标偏移变为 3，同时更新 k 的值： k=k−k/2=1。

由于 k 的值变成 1，因此比较两个有序数组中的未排除下标范围内的第一个数，其中较小的数即为第 k 个数，由于 A[3]>B[3]，因此第 kk 个数是 B[3]=4。

A: [1 3 4] 9
           ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

代码

public class FindMedianSortedArrays {
    public static void main(String[] args) {
        int[] nums1 = {1,2,3};
        int[] nums2 = {4,5,6,7,8,9,10,11,12,13,14,17};
        System.out.println(findMedianSortedArrays( nums1,  nums2));
    }
    public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            double median = getKthElement(nums1, nums2, midIndex + 1);
            return median;
        } else {
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
            return median;
        }
    }
    private static double getKthElement(int[] nums1, int[] nums2, int k) {
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */
        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {
            // 边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }

            // 正常情况
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

(LeetCode-33)搜索旋转排序数组

题目

整数数组 nums 按升序排列，数组中的值互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标从 0 开始计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你旋转后的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1 2	输入：nums = [4,5,6,7,0,1,2], target = 0 输出：4

示例 2：

1 2	输入：nums = [4,5,6,7,0,1,2], target = 3 输出：-1

示例 3：

1 2	输入：nums = [1], target = 0 输出：-1

分析

方法一：二分查找

思路和算法

对于有序数组，可以使用二分查找的方法查找元素。

但是这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。

可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：

如果 [l, mid - 1] 是有序数组，且 target 的大小满足 [nums[l],nums[mid])，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组，且 target 的大小满足 (nums[mid+1],nums[r]]，则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。

需要注意的是，二分的写法有很多种，所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别。

代码

public class MidSearch {
    public static void main(String[] args) {
        //int[] nums = {4,5,6,7,0,1,2};
        int[] nums = {3, 1};
       // int[] nums = {4,5,6,7,0,1,2};
        //int[] nums = {1};
        int a = new MidSearch().search(nums, 1);
        System.out.println();
    }

    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        return search1( nums, 0, nums.length - 1,  target);
    }

    public int search1(int[] nums, int start, int end, int target) {
        while (start <= end){
            int mid =  (end + start) / 2;
            if(nums[mid] == target){
                return mid;
            }
            if(nums[start] <= nums[mid]){
                // 判断是否在范围内
                if(nums[start] <= target && target < nums[mid]){
                    end = mid -1;
                }else {
                    start = mid + 1;
                }
            }else {
                if(nums[mid] < target && target <= nums[end]){
                    start = mid + 1;
                }else {
                    end = mid -1;
                }
            }
        }
        return -1;
    }
}

(LeetCode- 34) 在排序数组中查找元素的第一个和最后一个位置

题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1 2	输入：nums = [5,7,7,8,8,10], target = 8 输出：[3,4]

示例 2：

1 2	输入：nums = [5,7,7,8,8,10], target = 6 输出：[-1,-1]

示例 3：

1 2	输入：nums = [], target = 0 输出：[-1,-1]

分析

方法

由于数组已经排序，我们可以利用二分法来加速查找的过程。

代码

public class SearchRange {
    public static void main(String[] args) {
        int[] nums = {5,7,7,8,8,10};
        int[]  result = new SearchRange().searchRange( nums,  8);
        System.out.println("");
    }

    public int[] searchRange(int[] nums, int target) {
        int left =  searchLeft( nums,  0,  nums.length - 1,  target);
        int right =  searchRight( nums,  0,  nums.length - 1,  target);
        int[] result = {left, right};
        return result;
    }

    public int searchLeft(int[] nums, int start, int end, int target) {
        int idx = -1;
        while (start <= end){
            int mid = ( start + end ) / 2 ;
            if(nums[mid] >= target){
                end = mid - 1;
            }else {
                start = mid + 1;
            }
            if( nums[mid] == target){
                idx = mid;
            }
        }
        return idx;
    }

    public int searchRight(int[] nums, int start, int end, int target) {
        int idx = -1;
        while (start <= end){
            int mid = ( start + end ) / 2 ;
            if(nums[mid] > target){
                end = mid - 1;
            }else {
                start = mid + 1;
            }
            if( nums[mid] == target){
                idx = mid;
            }
        }
        return idx;
    }
}

(LeetCode- 153) 寻找旋转排序数组中的最小值

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。给你一个元素值互不相同的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

分析

代码

public class FindMin {
    public static void main(String[] args) {
    }
    public int findMin(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        int n = nums.length;
        int start = 0;
        int end = n - 1;
        while (start <= end){
            if(start + 1 == end){
                return Math.min(nums[start], nums[end]);
            }
            int mid = ( start + end ) / 2;
            if(nums[start] <= nums[mid] && nums[mid] <= nums[end]){
                return nums[start];
                //在左边
            }else if( nums[start] >= nums[mid] && nums[mid] < nums[end] ){
                end = mid ;
            }else{
                start = mid;
            }
        }
        return -1;
    }
}

(LeetCode- 240) 搜索二维矩阵 II

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

1 2	输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出：true

示例 2：

1 2	输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109

分析

方法三：Z 字形查找

思路与算法

我们可以从矩阵matrix 的右上角 (0,n−1) 进行搜索。在每一步的搜索过程中，如果我们位于位置(x,y)，那么我们希望在以 matrix 的左下角为左下角、以(x,y) 为右上角的矩阵中进行搜索，即行的范围为 [x, m - 1][x,m−1]，列的范围为 [0, y][0,y]：

如果 [x,y]=target，说明搜索完成；
如果 [x,y]>target，由于每一列的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 y 列的元素都是严格大于 target 的，因此我们可以将它们全部忽略，即将 y 减少 1；
如果 [x,y]<target，由于每一行的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 x 行的元素都是严格小于 target 的，因此我们可以将它们全部忽略，即将 x 增加 1。

在搜索的过程中，如果我们超出了矩阵的边界，那么说明矩阵中不存在 target。

代码

public class SearchMatrix {
    public static void main(String[] args) {
        int[][] matrix = {{1,4,7,11,15}, {2,5,8,12,19},{3,6,9,16,22}, {10,13,14,17,24},{18,21,23,26,30} };
        boolean  falew = new SearchMatrix().searchMatrix( matrix,  29);
        System.out.println(matrix.length);
    }
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix == null){
            return false;
        }
        // 矩阵行和列下标的最大值
        int cols = matrix[0].length-1;
        int rows = matrix.length-1;
        if(target > matrix[rows][cols]) {
            return false;
        }
        int currentCol = cols;
        int currentRow = 0;
        while (currentCol >= 0 && currentRow <= rows){
            if(target == matrix[currentRow][currentCol]){
                return true;
            }else if(target < matrix[currentRow][currentCol]){
                currentCol--;
            }else if(target > matrix[currentRow][currentCol]){
                currentRow++;
            }
        }
        return false;
    }
}

(LeetCode-1)两数之和

题目

分析

方法1

方法2

代码示例：

(LeetCode-88) 合并两个有序数组

题目

分析

方法1

方法2

代码示例

(LeetCode-283)移动零

题目

分析

方法

代码示例

(LeetCode-448)找到所有数组中消失的数字

题目

(LeetCode-169) 多数元素

题目

分析

方法1

方法2

(LeetCode-11) 盛最多水的容器

题目

分析

方法一：双指针

代码

(LeetCode-15) 三数之和

题目

分析

代码

(LeetCode-31)下一个排列

题目

分析

方法一：两遍扫描

代码

**(LeetCode-48) **旋转图像

题目

分析

方法：用翻转代替旋转

代码

**(LeetCode-54) **螺旋矩阵

题目

分析

方法二：按层模拟

代码

**(LeetCode-55) **跳跃游戏

题目

分析

方法1

方法2

代码

**(LeetCode-215)**数组中的第K个最大元素

题目

分析

方法一：基于快速排序的选择方法

代码

(LeetCode-347) 前 K 个高频元素

题目

分析

方法一：堆

代码

**(LeetCode-4) **寻找两个正序数组的中位数

题目

分析

方法一：二分查找

代码

(LeetCode-33)搜索旋转排序数组

题目

分析

方法一：二分查找

代码

(LeetCode- 34) 在排序数组中查找元素的第一个和最后一个位置

题目

分析

方法

代码

(LeetCode- 153) 寻找旋转排序数组中的最小值

(LeetCode-48) 旋转图像

(LeetCode-54) 螺旋矩阵

(LeetCode-55) 跳跃游戏

(LeetCode-215)数组中的第K个最大元素

(LeetCode-4) 寻找两个正序数组的中位数