AVL树本质还是一棵二叉查找树
1 概述
平衡二叉树是由前苏联的两位数学家G.M.Adelse-Velskil和E.M.Landis提出,因此一般也称作AVL树,AVL树本质还是一棵二叉查找树,只是在其基础上增加了“平衡”的要求。所谓平衡是指,对AVL树的任意结点来说,其左子树与右子树的高度之差的绝对值不超过1,其中左子树与右子树的高度因子之差称为平衡因子。
如下所示,就是一棵由{1,2,3,4,5,7,8}构建的AVL树:
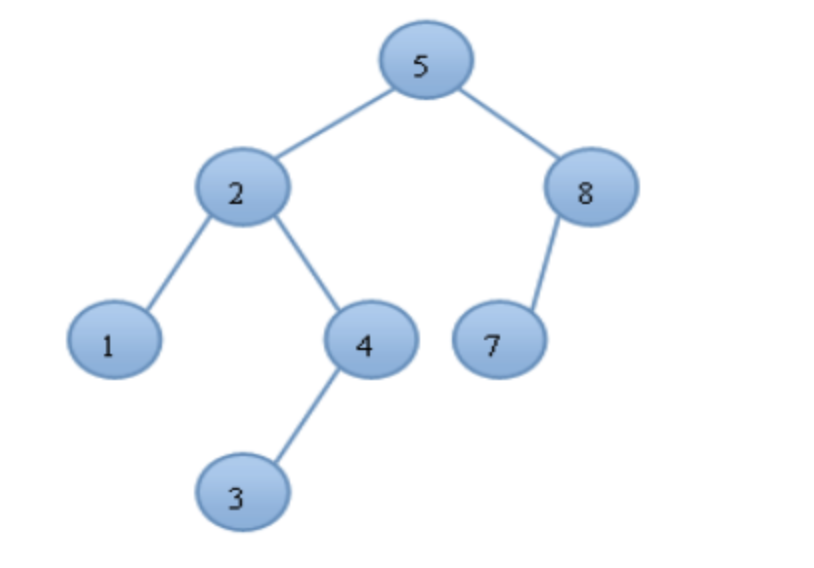
只要能随时保证每个结点平衡因子的绝对值不超过1,AVL的高度就始终能保持O(logn)级别,由于需要对每个结点都得到平衡因子,因此需要在树的结构中加入一个变量height来记录以当前结点为根结点的子树的高度。
2 创建
AVL树的创建是基于二叉查找树的插入代码的基础上,增加平衡操作的。需要从插入的结点开始从下往上判断结点是否失衡,因此,需要在调用insert函数以后,更新当前子树的高度,并在这之后根据树型来进行相应的平衡操作。那么,怎么进行平衡操作呢?AVL树的插入是需要采取左旋或者右旋操作的,即,插入后,由于插入操作,导致某棵子树的高度超过了另一棵子树高度的2个结点高度,这样就破坏了树的平衡性,需要做出调整。
2.1 右旋
如下所示一棵简单的AVL树,对其进行插入操作以后:
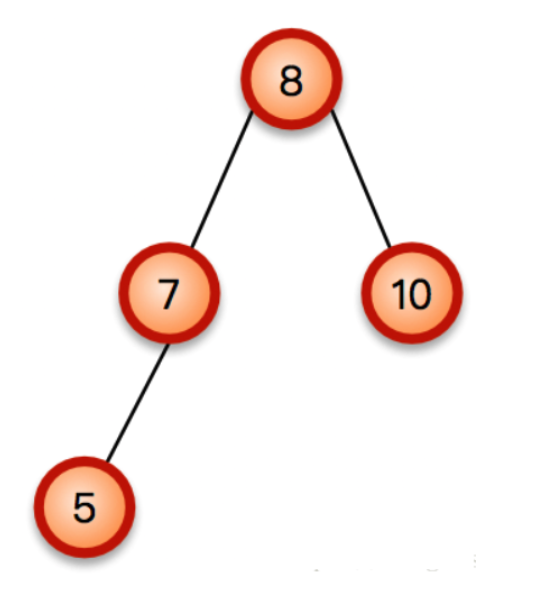
一棵简单的AVL树, 变成了下图这样的AVL树:
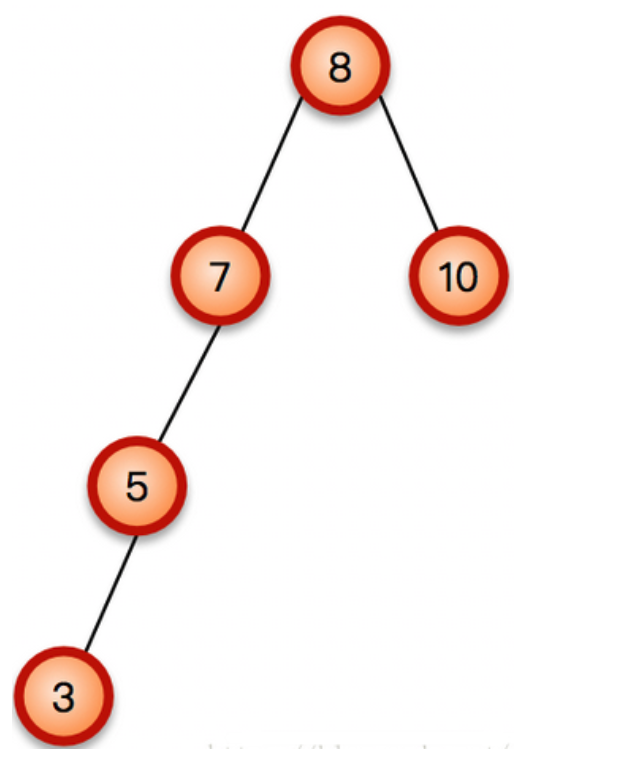
这样子就失衡了,所谓右旋操作,就是将这棵AVL树,从最靠近插入结点的失衡结点处,通过往右子树调整,使整棵树的每个结点的平衡因子变为正常,不如上图的树,离插入节点3最近的失衡结点是7,
则可以通过下图所示的操作,来平衡二叉树,即调整整棵树平衡因子:
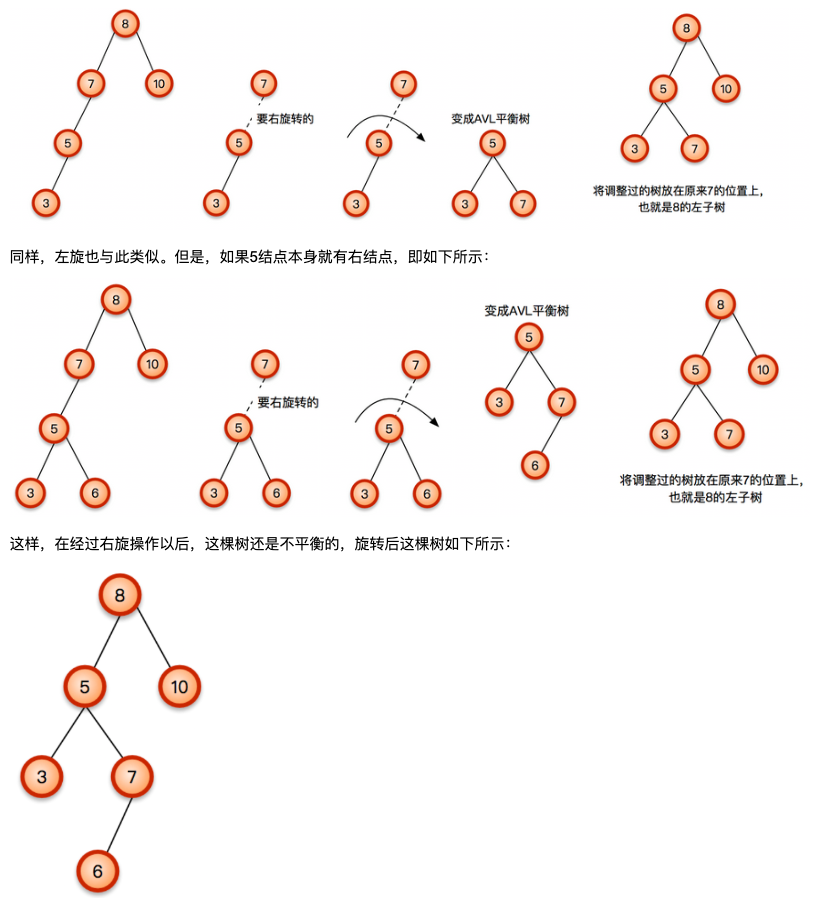
因此,还需要进行一次旋转,显然,继续右旋已经无法满足我们的需求,那么要如何进行操作,才能使这棵树回复平衡呢?(在后续中,会进行讲解)
2.2 左旋操作
左旋操作与右旋操作是类似的,都属于对子树的单旋转。
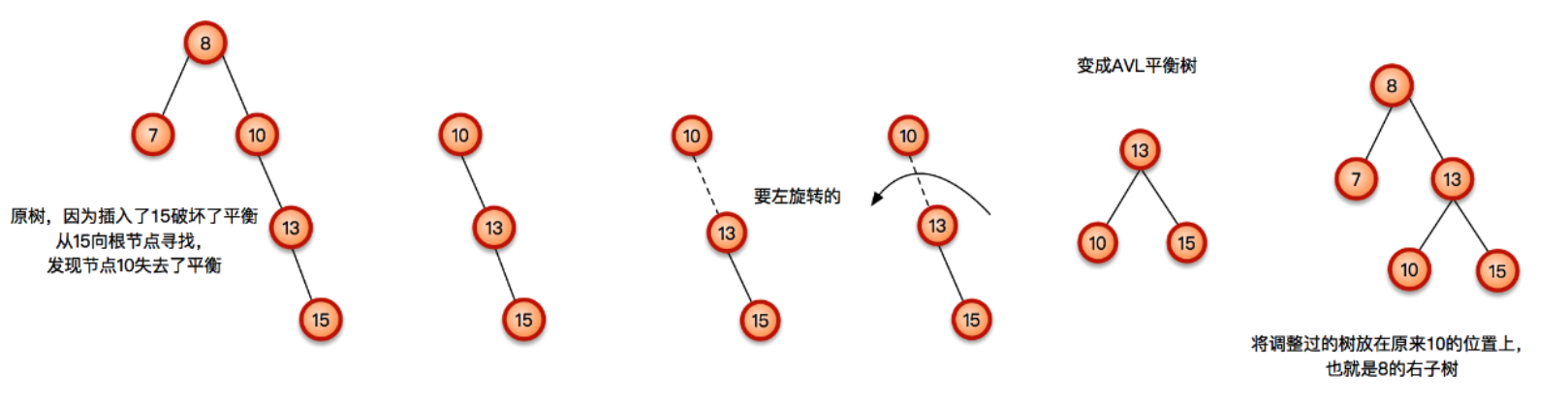
左旋与右旋一样,同样也存在这样的问题,如果该树的右子树的左结点存在,则单一通过左旋是做不到的,那么应该如何处理呢?
其实,以L和R来表示,插入结点的位置,有以下四种情况:
| 插入方式 |
描述 |
旋转方式 |
| LL |
在a的左子树根节点的左子树上插入节点而破坏平衡 |
右旋转 |
| RR |
在a的右子树根节点的右子树上插入节点而破坏平衡 |
左旋转 |
| LR |
在a的左子树根节点的右子树上插入节点而破坏平衡 |
先左旋后右旋 |
| RL |
在a的右子树根节点的左子树上插入节点而破坏平衡 |
先右旋后左旋 |
从上表可以看出,左旋和右旋两种情况中,左右结点若存在的话,就是上表中的RL和LR情况。则,只需要对两种情况分别按照上表采取相应的操作就可以解决,如下图所示:
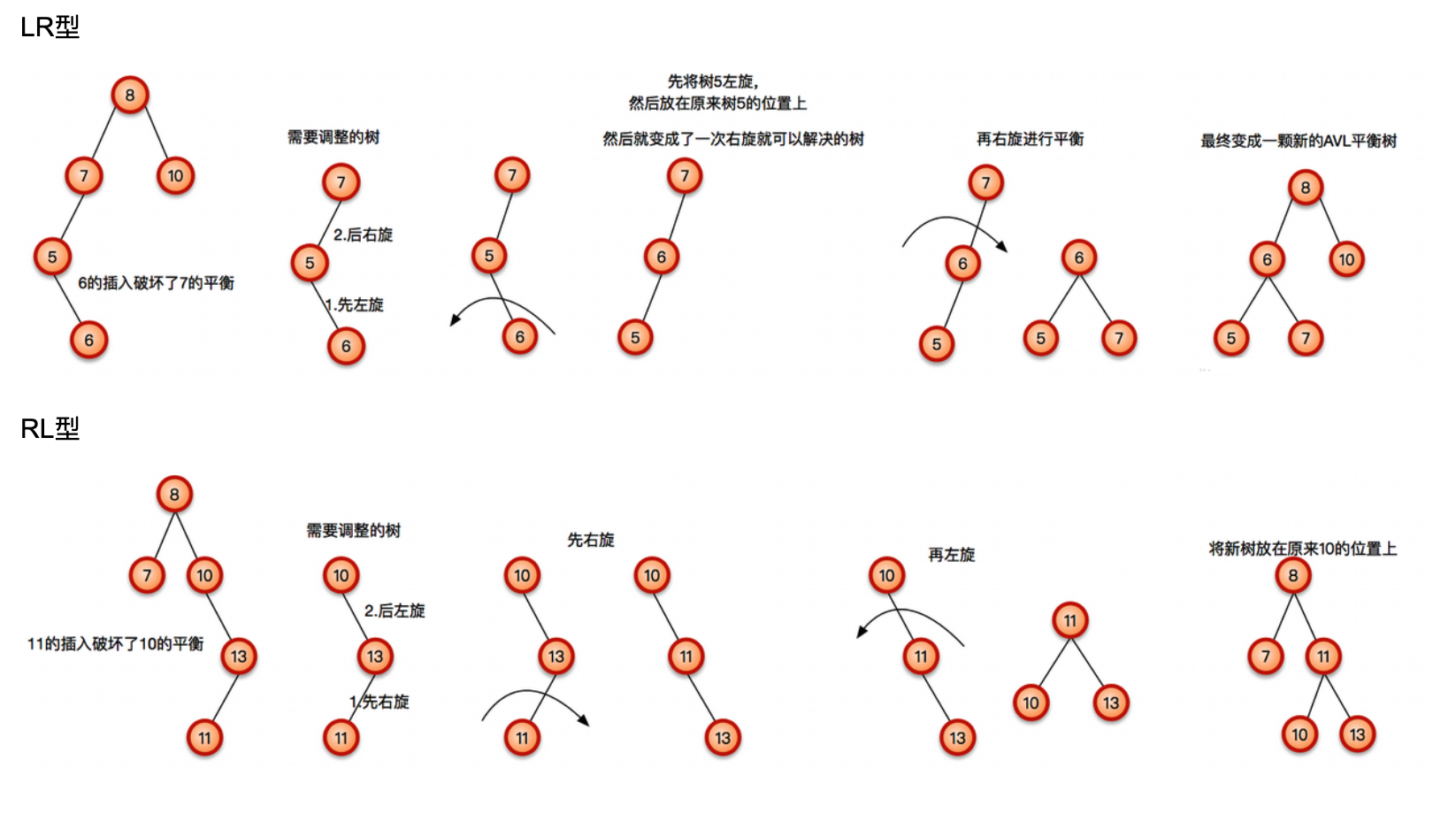
3 AVL代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
|
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
public int leftHeight(){
if(left == null){
return 0;
}
return left.height();
}
public int rightHeight(){
if(right == null){
return 0;
}
return right.height();
}
public int height(){
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height() ) + 1;
}
private void leftRotate(){
Node newNode = new Node(value);
newNode.left = left;
newNode.right = right.left;
value = right.value;
right = right.right;
left = newNode;
}
public void rightRotate(){
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
public void add(Node node){
if(node == null){
return;
}
if(node.value < this.value){
if(this.left == null){
this.left = node;
}else{
this.left.add(node);
}
}else{
if(this.right == null){
this.right = node;
}else{
this.right.add(node);
}
}
if(rightHeight() - leftHeight() > 1){
if(right != null && right.leftHeight() > left.rightHeight()){
right.rightRotate();
}
leftRotate();
}
if(leftHeight() - rightHeight() > 1){
if(left != null && left.rightHeight() > left.leftHeight()){
left.leftRotate();
}
rightRotate();
}
}
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null){
this.right.infixOrder();
}
}
public Node search(int value){
if(value == this.value){
return this;
}else if(value < this.value){
if(this.left != null){
return this.left.search(value);
}
}else{
if(this.right != null){
return this.right.search(value);
}
}
return null;
}
public Node searchParent(int value){
if(this.left != null && this.left.value == value || (this.right != null && this.right.value == value)){
return this;
}else {
if(value < this.value && this.left != null){
return this.left.searchParent(value);
}else if(value >= this.value && this.right != null){
return this.right.searchParent(value);
}else{
return null;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
|
class AVLTree{
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
public void add(Node node){
if(root == null){
root = node;
}else{
root.add(node);
}
}
public void infixOrder(){
if(root != null){
root.infixOrder();
}else{
System.out.println("数为null");
}
}
public Node search(int value){
if(null == root){
return null;
}else{
return root.search(value);
}
}
public Node searchParent(int value){
if(null == root){
return null;
}else{
return root.searchParent(value);
}
}
public int delRightTreeMin(Node node){
Node target = node;
while(target.left != null){
target = target.left;
}
delNode(target.value);
return target.value;
}
public void delNode(int value){
if(null == root){
return ;
}else{
Node targetNode = search(value);
if(null == targetNode){
return ;
}
if(null == root.left && null == root.right){
root = null;
return ;
}
Node parent = searchParent(value);
if(null == targetNode.left && null == targetNode.right){
if(parent.left != null && parent.left.value == value){
parent.left = null;
}else if(parent.right != null && parent.right.value == value){
parent.right = null;
}
}else if(targetNode.left != null && targetNode.right != null){
int minValue = delRightTreeMin(targetNode.right);
targetNode.value = minValue;
}else{
if(targetNode.left != null){
if(parent.left.value == value){
parent.left = targetNode.left;
}else{
parent.right = targetNode.right;
}
}else{
if(parent.left.value == value){
parent.left = targetNode.right;
}else{
parent.right = targetNode.right;
}
}
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public class AVLTreeDemo {
public static void main(String[] args) {
int[] arr = {10,11,7,6,8,9};
AVLTree avlTree = new AVLTree();
for(int i = 0; i < arr.length; i++){
avlTree.add(new Node(arr[i]));
}
System.out.println("树的高度 " + avlTree.getRoot().height());
System.out.println("树的左子树高度 " + avlTree.getRoot().leftHeight());
System.out.println("树的右子树高度 " + avlTree.getRoot().rightHeight());
avlTree.infixOrder();
}
}
|





