Hexo

点滴积累 豁达处之

0%

07 数据结构-赫夫曼树

Posted on Edited on In
数据结构与算法

赫夫曼树，别名“哈夫曼树”、“最优树”以及“最优二叉树”

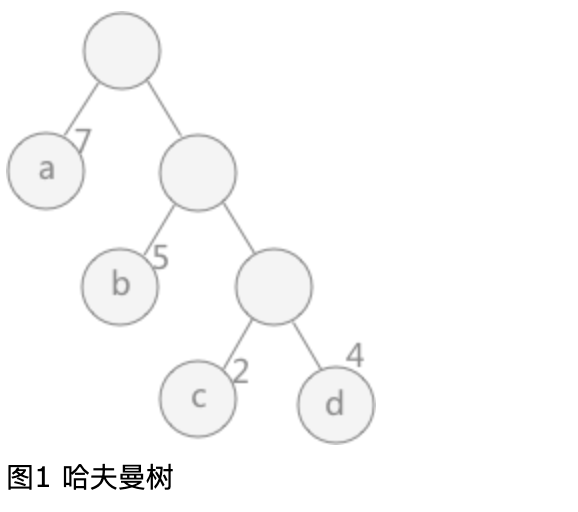
1 概念

路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。图 1 中，从根结点到结点 a 之间的通路就是一条路径。

路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。

结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。例如，图 1 中结点 a 的权为 7，结点 b 的权为 5。

结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如，图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。

树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为：WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

Structure_huffmanTree1

2 什么是赫夫曼树

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。

在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。在图 1 中，因为结点 a 的权值最大，所以理应直接作为根结点的孩子结点。

3 构建哈夫曼树

对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：

  1. 在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
  2. 在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；
  3. 重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

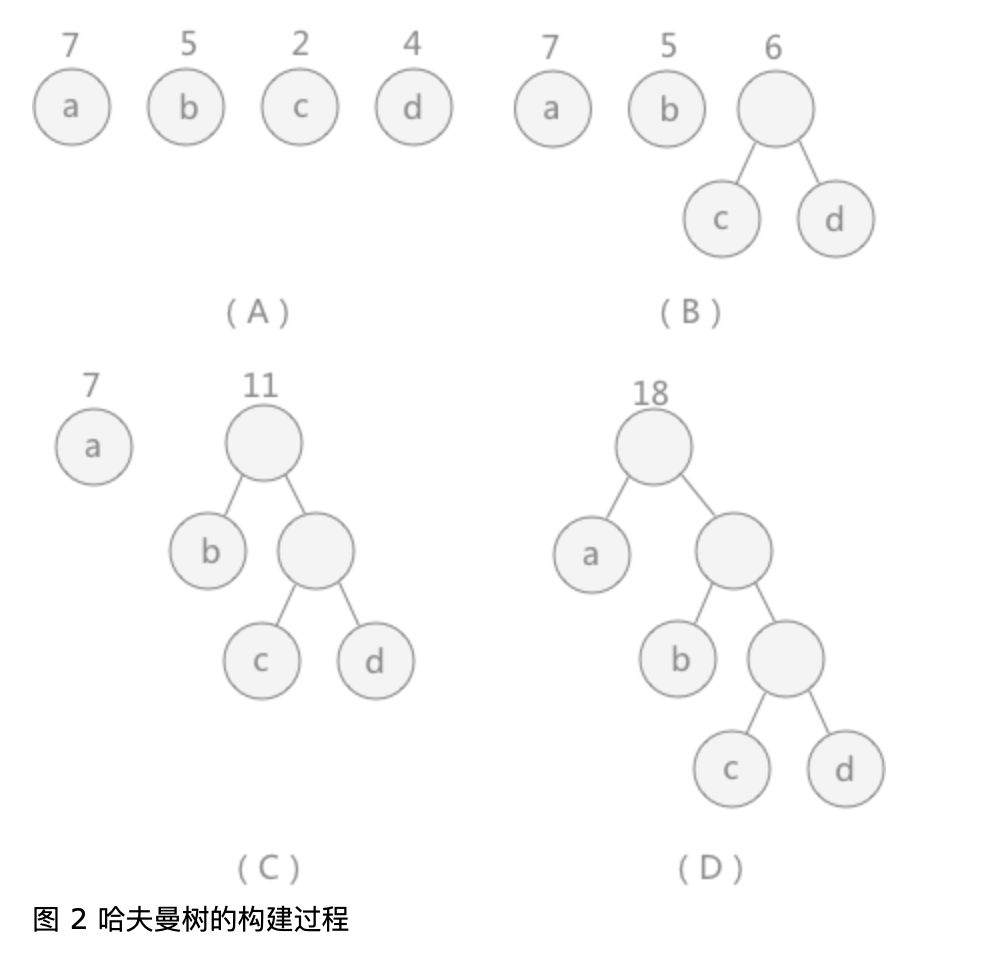
Structure_hufmantree2

​ 图 2 中，（A）给定了四个结点a，b，c，d，权值分别为7，5，2，4；第一步如（B）所示，找出现有权值中最小的两个，2 和 4 ，相应的结点 c 和 d 构建一个新的二叉树，树根的权值为 2 + 4 = 6，同时将原有权值中的 2 和 4 删掉，将新的权值 6 加入；进入（C），重复之前的步骤。直到（D）中，所有的结点构建成了一个全新的二叉树，这就是哈夫曼树。

​ 构建哈夫曼树时，首先需要确定树中结点的构成。由于哈夫曼树的构建是从叶子结点开始，不断地构建新的父结点，直至树根，，因此每个结点需要有指向其左孩子和右孩子的指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
//创建赫夫曼树
    public static Node createHuffmanTree(int[] arr){
        //1，遍历arr数组
        //2，将arr的每个元素构成一个Node
        //3，将Node放入到ArrayList中
        List<Node> nodes = new ArrayList<>();
        for(int value : arr){
            nodes.add(new Node(value));
        }

        while(nodes.size() > 1){
            //排序
            Collections.sort(nodes);

            //取出权值最小的二叉树
            Node left = nodes.get(0);
            Node right = nodes.get(1);
            //构建一颗新的二叉树
            Node parent = new Node(left.value + right.value);
            parent.left = left;
            parent.right = right;
            //从ArrayList中删除使用过的二叉树
            nodes.remove(left);
            nodes.remove(right);
            //将parent加入到到ArrayList中
            nodes.add(parent);
        }
        return nodes.get(0);
    }

//创建节点类
class Node implements Comparable<Node>{
    int value; //节点权值
    Node left; //指向左子节点
    Node right; //指向右子节点

    //前序遍历
    public  void preOrder(){
        System.out.println(this);
        if(this.left != null){
            this.left.preOrder();
        }
        if(this.right != null){
            this.right.preOrder();
        }
    }

    public Node(int value){
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    @Override
    public int compareTo(Node o) {
        return this.value - o.value;
    }
}

4 赫夫曼编码

​ 哈夫曼编码就是在哈夫曼树的基础上构建的，这种编码方式最大的优点就是用最少的字符包含最多的信息内容。

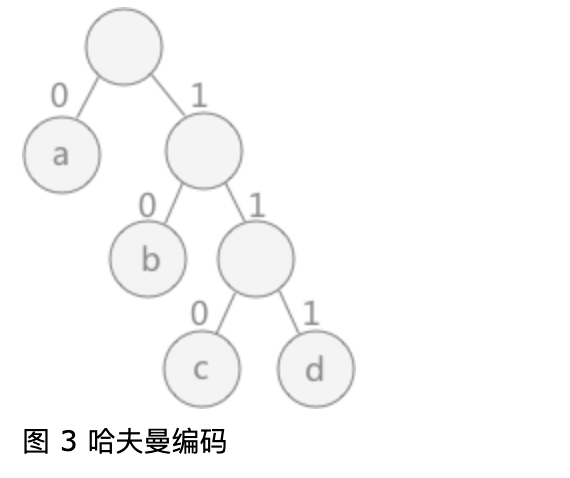
​ 根据发送信息的内容，通过统计文本中相同字符的个数作为每个字符的权值，建立哈夫曼树。对于树中的每一个子树，统一规定其左孩子标记为 0 ，右孩子标记为 1 。这样，用到哪个字符时，从哈夫曼树的根结点开始，依次写出经过结点的标记，最终得到的就是该结点的哈夫曼编码。

Structure_huffmantree4

如图 3 所示，字符 a 用到的次数最多，其次是字符 b 。字符 a 在哈夫曼编码是 0 ，字符 b 编码为 10 ，字符 c 的编码为 110 ，字符 d 的编码为 111 。

赫夫曼编码完整代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//节点类
class Node implements Comparable<Node>{
    Byte data; //存放的数据
    int weight; //权重，表示字符出现的次数
    Node left;
    Node right;

    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight - o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }

    //前序遍历
    public  void preOrder(){
        System.out.println(this);
        if(this.left != null){
            this.left.preOrder();
        }
        if(this.right != null){
            this.right.preOrder();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
public class HuffmanCode {

    public static void main(String[] args) {
        String str = "i like like like java do you like a java";
        byte[] contentBytes = str.getBytes();

        byte[] huffmanCodesBytes = huffmanZip(contentBytes);
        System.out.println("huffmanBodeByte: " + 		Arrays.toString(huffmanCodesBytes));

        byte[] bytes = decode(huffmanCodes, huffmanCodesBytes);
        System.out.println(new String(bytes));
    }

    //解码

    /**
     *
     * @param huffmanCodes  huffman编码表
     * @param huffmanBytes 编码过的字节数组
     * @return 返回原来字符串对应的数组
     */
    private static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes){
        //1，先得到huffmanBytes 对应的二进制字符串，形式10100100100010101001
        StringBuilder stringBuilder = new StringBuilder();

        //2,将byte【】 转成二进制的字符串
        for(int i = 0; i < huffmanBytes.length; i++){
            byte b = huffmanBytes[i];
            //判断是不是最后一个字节
            boolean flag = (i == huffmanBytes.length - 1);
            stringBuilder.append(byteToBitString(!flag, b));
        }
      //  System.out.println(stringBuilder.toString());

        //把字符串按指定的Huffman编码进行解码
        //把Huffman编码进行调换，因为反向查询
        Map<String, Byte> map = new HashMap<>();
        for(Map.Entry<Byte, String> entry : huffmanCodes.entrySet()){
            map.put(entry.getValue(), entry.getKey());
        }
     //   System.out.println(map);

        //创建集合，存放byte
        List<Byte> list = new ArrayList<>();
        for(int i = 0; i < stringBuilder.length();){
            int count = 1; //小的计数器
            boolean flag = true;
            Byte b = null;

            while(flag){
                //  取出一个1或0
                String key = stringBuilder.substring(i, i+count);//i不动，count移动，直到匹配到一个字符
                b = map.get(key);
                if(null == b){
                    count++;
                }else{

                    flag = false;
                }
            }
            list.add(b);
            i += count; //i直接移动到count位置
        }

        byte[] by = new byte[list.size()] ;
        for(int i = 0; i < by.length; i++){
            by[i] = list.get(i);
        }
        return by;
    }


    /**
     * 将一个byte转成一个二进制的字符串
     * @param b
     * @param flag 标记是否需要补高位 true：补(最后一个不需补高位)
     * @return 是该b 对应的二进制的字符串，（按补码返回）
     */
    private static String byteToBitString(boolean flag , byte b){
        //使用变量保存b
        int temp = b; //将b转成 int

        if(flag){
            //如果是正数，补高位
            temp |= 256;
        }

        String str = Integer.toBinaryString(temp);
        if(flag){
            return str.substring(str.length() - 8);
        }else{
            return  str;
        }
    }

    /**
     * 将前面的方法封装起来，便于调用
     * @param bytes 原始的字符串对应的字节数字
     * @return 返回经过Huffman编码处理后的字节数组（压缩后的数组）
     */
    private static byte[] huffmanZip(byte[] bytes){

        List<Node> nodes = getNodes(bytes);
        //根据Nodes创建Huffman树
        Node node = createHuffmanTree(nodes);
        ////生成对应的Huffman编码
        Map<Byte, String>  huffmanCodes = getCodes(node);
        //压缩
        byte[] huffmanCodesBytes = zip(bytes, huffmanCodes);

        return huffmanCodesBytes;
    }

    /**
     * 编写方法，将字符串对应的byte[]数组，通过生成的Huffman编码表，返回一个Huffman编码压缩后的byte数组
     * @param bytes 原始的字符串对应的bytes
     * @param huffmanCodes 生成的Huffman编码
     * @return 返回Huffman编码处理后的byte[]。8位对应一个byte放入到byte数组中
     * huffmanCodeByte[0] = 10101000 => byte
     */
    private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes){
        //1,先利用Huffman编码表，将bytes转成Huffman编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();

        //遍历byte数组
        for(byte b : bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
      //  System.out.println(stringBuilder.toString());
        //将"1010010100101001010010100101010转成byte数组
        //统计返回byte[]长度
        int len;
        if(stringBuilder.length() % 8 == 0  ){
            len = stringBuilder.length() / 8;
        }else{
            len = stringBuilder.length() / 8 + 1;
        }
        //创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0; //记录第一个byte
        for(int i = 0; i < stringBuilder.length(); i+=8){ //每8位对应一个byte
            String stringByte ;
            if(i + 8 > stringBuilder.length()){ //不够8位
                stringByte = stringBuilder.substring(i );
            }else{
                stringByte = stringBuilder.substring(i , i+8);
            }
            //将strByte转成一个byte， 放入到huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(stringByte, 2);
            index++;
        }
        return huffmanCodeBytes;
    }

    //生成赫夫曼树对应的赫夫曼编码
    //1，将赫夫曼编码表存放在Map<Byte, String> 形式
    // 32-> 01  97->100  100->1100等等
    static Map<Byte,String> huffmanCodes = new HashMap<>();
    //2, 在生成赫夫曼编码表时需要拼接路径。定义一个StringBuilder存储某个叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();

    //为了调用方便
    private static Map<Byte, String> getCodes(Node node){
        if(null == node){
            return null;
        }
        //处理root的左子树
        getCodes(node.left, "0", stringBuilder);
        //处理右子树
        getCodes(node.right, "1", stringBuilder);

        return  huffmanCodes;
    }
    /**
     * 将传入的Node节点的所有叶子节点的Huffman编码，存放到huffmanCodes集合
     * @param node 传入节点
     * @param code 路径 左子节点是0 右子节点是1
     * @param stringBuilder 用于拼接路径
     */
    private static void getCodes(Node node, String code, StringBuilder stringBuilder){
        StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
        //将code加入到stringBuilder2中
        stringBuilder2.append(code);
        if(node != null){ //如果node == null 不处理
            //判断当前弄得是叶子节点还是非叶子节点
            if(node.data == null){//非叶子节点
                //递归处理
                //向左递归
                getCodes(node.left, "0", stringBuilder2);
                //向右递归
                getCodes(node.right, "1", stringBuilder2);
            }else {//说明是叶子节点
                //就表示找到某个叶子节点的最后
                huffmanCodes.put(node.data, stringBuilder2.toString());
            }
        }
    }

    //
    private static void preOrder(Node node){
        if(null != node){
            node.preOrder();
        }
    }

    /**
     *
     * @param bytes 接收字符数组
     * @return 返回的就是List形式
     */
    public static List<Node> getNodes(byte[] bytes){
        //创建ArrayList
        List<Node> nodes = new ArrayList<>();
        //存储每个byte出现的次数
        Map<Byte, Integer> map = new HashMap<Byte, Integer>();
        for(byte b : bytes){
            if(null == map.get(b) ){
                map.put(b,1);
            }else{
                map.put(b, map.get(b) + 1);
            }
        }

        //把每个键值对转成Node对象，并加入到nodes集合
        for(Map.Entry<Byte, Integer> entry :   map.entrySet()){
            nodes.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodes;
    }

    /**
     *
     * @param nodes
     * @return 返回赫夫曼树根节点
     */
    private static  Node createHuffmanTree(List<Node> nodes){
        while(nodes.size() > 1){
            //从小到大
            Collections.sort(nodes);

            Node left = nodes.get(0);
            Node right = nodes.get(1);
            Node parent = new Node(null,left.weight + right.weight);
            parent.left = left;
            parent.right = right;

            nodes.remove(left);
            nodes.remove(right);
            nodes.add(parent);
        }
        return  nodes.get(0);
    }
}