经典算法-汉诺塔问题

问题是源于印度一个古老传说的益智玩具。 。。

1 概述

>法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

文章中我们假设汉诺塔个数为正整数n，三个盘子为A,B,C,其中C是中介盘，我们要遵守移动规则将A上的盘子要全部通过C移动到B。

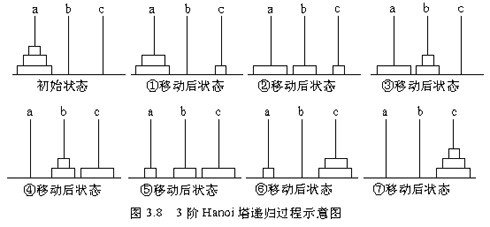
​ 如果汉诺塔上盘子个数n=1时显然直接将A上的盘子移动到B即可，当n=2时，方法也很简单,只要将第一块盘子先从A移动到C,再将第二块盘子从A移动到B,再将第一块盘子从C移动到A。实际上，表达的时候不必要强调第几块盘子，而只需要像从A移动到B这样描述,也能清楚的知道意思(因为总是只能移动每个汉诺塔最顶上的盘子)。那么n=2时解决办法的表示就是:A->C,A->B,C->B。下面我们都采用这种简洁明了的表示。

​ 要知道如何将n块盘子从A通过C移动到B，我们可以先将上面的n-1块盘子从A通过B移动到C，再将最大的盘子从A移动到B,这时再将上面的n-1块盘子从C通过A移动到B。这就是递归算法解决Hanoi塔问题的思路

2 递归实现

递归代码思想：永远把它想象为只有一个或两个盘子

/**
     * 将A汉诺塔上的n个盘子通过C移动到B的递归方法
     * @param n   //汉诺塔上盘子的个数
     * @param A   //开始时有盘子的汉诺塔
     * @param B   //要将盘子移动到上面的目标汉诺塔
     * @param C   //中介汉诺塔
     * @throws IllegalArgumentException when n<=0
     */
    public static void HanoiTowers1(int n,char A,char B,char C){
        if(n<=0){
            throw new IllegalArgumentException("n must be >=1");
        }
        if(n==1){
            System.out.println(A+"->"+B);
        }
        else{
            HanoiTowers1(n-1,A,C,B);     // 将除去最大的盘子的n个盘子从A通过B移动到C
            System.out.println(A+"->"+B);//将最大的盘子从A移动到B
            HanoiTowers1(n-1,C,B,A);     //将除去最大的盘子的n-1个盘子从C通过A移动到B
        }
    }

    public static void HanoiTowers1(int n){
        HanoiTowers1(n,'A','B','C');
    }

参考链接