排序-08 基数排序

基数排序与本系列前面讲解的七种排序方法都不同，它不需要比较关键字的大小。

它是根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。

1 示例

通过一个具体的实例来展示一下，基数排序是如何进行的。

设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。

我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以0~9来表示的。

所以我们不妨把0~9视为10个桶。

我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是0，将这个数存入编号为0的桶中。

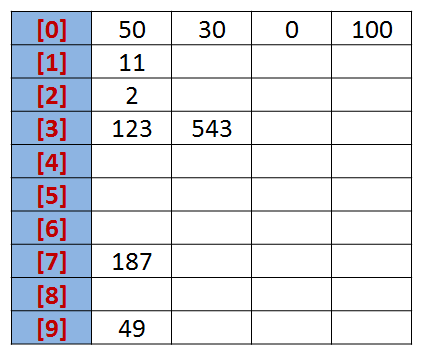
分类后，我们在从各个桶中，将这些数按照从编号0到编号9的顺序依次将所有数取出来。

这时，得到的序列就是个位数上呈递增趋势的序列。

按照个位数排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。

接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。

public class RadixSort {
 
    // 获取x这个数的d位数上的数字
    // 比如获取123的1位数，结果返回3
    public int getDigit(int x, int d) {
        int a[] = {
                1, 1, 10, 100
        }; // 本实例中的最大数是百位数，所以只要到100就可以了
        return ((x / a[d]) % 10);
    }
 
    public void radixSort(int[] list, int begin, int end, int digit) {
        final int radix = 10; // 基数
        int i = 0, j = 0;
        int[] count = new int[radix]; // 存放各个桶的数据统计个数
        int[] bucket = new int[end - begin + 1];
 
        // 按照从低位到高位的顺序执行排序过程
        for (int d = 1; d <= digit; d++) {
 
            // 置空各个桶的数据统计
            for (i = 0; i < radix; i++) {
                count[i] = 0;
            }
 
            // 统计各个桶将要装入的数据个数
            for (i = begin; i <= end; i++) {
                j = getDigit(list[i], d);
                count[j]++;
            }
 
            // count[i]表示第i个桶的右边界索引
            for (i = 1; i < radix; i++) {
                count[i] = count[i] + count[i - 1];
            }
 
            // 将数据依次装入桶中
            // 这里要从右向左扫描，保证排序稳定性
            for (i = end; i >= begin; i--) {
                j = getDigit(list[i], d); // 求出关键码的第k位的数字， 例如：576的第3位是5
                bucket[count[j] - 1] = list[i]; // 放入对应的桶中，count[j]-1是第j个桶的右边界索引
                count[j]--; // 对应桶的装入数据索引减一
            }
 
            // 将已分配好的桶中数据再倒出来，此时已是对应当前位数有序的表
            for (i = begin, j = 0; i <= end; i++, j++) {
                list[i] = bucket[j];
            }
        }
    }
 
    public int[] sort(int[] list) {
        radixSort(list, 0, list.length - 1, 3);
        return list;
    }
 
    // 打印完整序列
    public void printAll(int[] list) {
        for (int value : list) {
            System.out.print(value + "\t");
        }
        System.out.println();
    }
 
    public static void main(String[] args) {
        int[] array = {
                50, 123, 543, 187, 49, 30, 0, 2, 11, 100
        };
        RadixSort radix = new RadixSort();
        System.out.print("排序前:\t\t");
        radix.printAll(array);
        radix.sort(array);
        System.out.print("排序后:\t\t");
        radix.printAll(array);
    }
}

运行结果：

1 2	排序前: 50 123 543 187 49 30 0 2 11 100 排序后: 0 2 11 30 49 50 100 123 187 543

2 算法分析

排序类型	排序方法	平均情况	最坏情况	最好情况	空间复杂度	稳定性	复杂度
基数排序	基数排序	O(d(n+r))	O(d(n+r))	O(d(n+r))	O(n+r)	稳定	较复杂

时间复杂度

通过上文可知，假设在基数排序中，r为基数，d为位数。则基数排序的时间复杂度为**O(d(n+r))**。

我们可以看出，基数排序的效率和初始序列是否有序没有关联。

空间复杂度

在基数排序过程中，对于任何位数上的基数进行“装桶”操作时，都需要n+r个临时空间。

算法稳定性

在基数排序过程中，每次都是将当前位数上相同数值的元素统一“装桶”，并不需要交换位置。所以基数排序是稳定的算法。

参考链接