栈的主要机制可用数组来实现,也可以用链表来实现。优先级队列的内部实现可以用数组或者一种特别的树——堆来实现。
1 栈的基本概念
数组、链表、树等数据结构适用于存储数据库应用中的数据记录,它们常常用于记录那些现实世界的对象和活动的数据,便与数据的访问:插入、删除和查找特定数据项
而栈和队列更多的是作为程序员的工具来使用。他们主要作为构思算法的辅助工具,而不是完全的数据存储工具。这些数据结构的生命周期比那些数据库类型的结构要短很多。在程序操作执行期间它们才被创建,通常它们去执行某项特殊的任务,当任务完成后就被销毁
栈和队列的访问是受限制的,即在特定时刻只有一个数据项可以被读取或删除
栈和队列是比数组和其他数据结构更加抽象的结构,是站在更高的层面对数据进行组织和维护
栈的主要机制可用数组来实现,也可以用链表来实现。优先级队列的内部实现可以用数组或者一种特别的树——堆来实现。
先来了解栈的概念和实例,然后分别深入理解队列和优先级队列
栈只允许访问一个数据项:即最后插入的数据。移除这个数据项后才能访问倒数第二个插入的数据项。它是一种“后进先出”的数据结构
栈最基本的操作是出栈(Pop)、入栈(Push),还有其他扩展操作,如查看栈顶元素,判断栈是否为空、是否已满,读取栈的大小等
2 基本的栈操作封装类
下面我们就用数组来写一个栈操作的封装类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class Stack {
private int size;
private int top;
private int [] stackArray;
public Stack(int size){
stackArray = new int [size];
top = -1;
this.size = size;
}
public void push(int elem){
stackArray[++top] = elem;
}
public int pop(){
return stackArray[top--];
}
public int peek(){
return stackArray[top];
}
public boolean isEmpty(){
return (top == -1);
}
public boolean isFull(){
return (top == size-1);
}
}
|
上例中,没有对可能的异常进行处理,需要由编程人员保证程序的正确性,比如,才出栈前需要应该保证栈中有元素,在入栈前应保证栈没有满
3 入栈出栈示意图
入栈示意图:
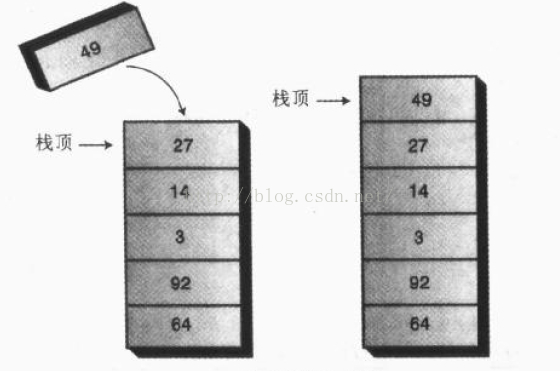
出栈示意图:

栈通常用于解析某种类型的文本串。通常,文本串是用计算机语言写的代码行,而解析它们的程序就是编译器
4 栈的应用-中缀表达式转为后缀表达式计算四则运算
4.1 前,中,后缀表达式
- 前缀表达式(Prefix Notation)是指将运算符写在前面操作数写在后面的不包含括号的表达式,而且为了纪念其发明者波兰数学家Jan Lukasiewicz所以前缀表达式也 叫做“波兰表达式”。比如- 1 + 2 3
- 后缀表达式(Postfix Notation)与之相反,是指运算符写在操作数后面的不含括号的算术表达式,也叫做逆波兰表达式。比如1 2 3 + -
不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则,如:2 1 + 3 *
- 中缀表达式(Infix Notation)就是常用的将操作符放在操作数中间的算术表达式。前缀表达式和后缀表达式相对于中缀表达式最大的不同就是去掉了表示运算优先级 的括号,比如1-2+3
在中缀表达式的情况下求值,既要考虑括号,优先级,还要考虑操作出现的先后顺序。但是,作为计算机,其计算过程就显的比较复杂,对于一个中缀表达式,需要不停地对表达式进行多次遍历,来查找相应的计算的信息。这样从算法复杂度上来说,是不可取的。前缀表达式和后缀表达式相对于人们常用的中缀表达式最大的不同就在于表达式中的运算符是按照一定的顺序出现(接下来会具体讲解),所以求值过程中并不需要在表达式中使用括号来指定运算顺序,也不需要在计算过程中其中考虑运算符号的优先级。在采用辅助数据结构的情况下,只需要对表达式进行一次遍历即可计算出结果,大大降低了算法复杂度,也更加符合传统计算机的工作方式。
4.2 采用中缀表达式的算法分析
4.2.1 将中缀表达式转换为后缀表达式:eg:
当读到数字直接送至输出队列中;
当读到运算符t时:
a.将栈中所有优先级高于或等于t的运算符弹出,送到输出队列中;
这句话不好理解,可以说成这样,从栈顶开始,依次弹出比当前处理的运算符优先级高的运算符,直到一个比它优先级低的或者遇到了一个左括号就停止。
b.t进栈;
读到左括号时总是将它压入栈中;
读到右括号时,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号;
中缀表达式全部读完后,若栈中仍有运算符,将其送到输出队列中。
4.2.2 中缀表达式转换为后缀表达式的过程:
运算示例: 3+(2-5)*6/3 :
| 后缀表达式 |
栈 |
| 3 |
|
| 3 |
+ |
| 3 |
+( |
| 32 |
+( |
| 32 |
+( - |
| 325 |
+( - |
| 325- |
+ |
| 325- |
+* |
| 325-6 |
+* |
| 325-6* |
+/ |
| 325-6*3 |
+/ |
| 325-6*3/+ |
|
最终后缀表达式为:325-6*3/+
4.2.3 运用后缀表达式进行计算:
- 建立一个栈S;
- 从左到右读后缀表达式,读到数字就将它转换为数值压入栈S中,读到运算符则从栈中依次弹出两个数分别到Y和X,然后以“X 运算符 Y”的形式计算机出结果,再压加栈S中;
- 如果后缀表达式未读完,就重复上面过程,最后输出栈顶的数值则为结束。
3+(2-5)6/3=-3 ,其后缀表达式为:325-63/+
运算过程如下:
| 栈 |
运算 |
| 3 2 5 |
325入栈 |
| 3 |
2-5=-3 |
| 3 -3 |
运算结果进栈 |
| 3 -3 6 |
|
| 3 |
-3*6=-18 |
| 3 -18 3 |
-18/3=-6 |
| 3 -6 |
3+(-6)=-3 |
| -3 |
|
5 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
| import java.util.Stack;
import java.util.regex.Pattern;
import static java.util.regex.Pattern.*;
public class StringToArithmetic {
public StringToArithmetic() {
}
public static double stringToArithmetic(String string) {
return suffixToArithmetic(infixToSuffix(string));
}
public static String infixToSuffix(String exp) {
Stack<Character> s = new Stack<Character>();
String suffix = "";
int length = exp.length();
for (int i = 0; i < length; i++) {
char temp;
char ch = exp.charAt(i);
switch (ch) {
case ' ':
break;
case '(':
s.push(ch);
break;
case '+':
case '-':
while (s.size() != 0) {
temp = s.pop();
if (temp == '(') {
s.push('(');
break;
}
suffix += temp;
}
s.push(ch);
break;
case '*':
case '/':
while (s.size() != 0) {
temp = s.pop();
if (temp == '+' || temp == '-' || temp == '(') {
s.push(temp);
break;
} else {
suffix += temp;
}
}
s.push(ch);
break;
case ')':
while (!s.isEmpty()) {
temp = s.pop();
if (temp == '(') {
break;
} else {
suffix += temp;
}
}
break;
default:
suffix += ch;
break;
}
}
while (s.size() != 0) {
suffix += s.pop();
}
return suffix;
}
public static double suffixToArithmetic(String exp) {
Pattern pattern = compile("\\d+||(\\d+\\.\\d+)");
String[] strings = exp.split("");
Stack<Double> stack = new Stack<Double>();
for (int i = 0; i < strings.length; i++) {
if (strings[i].equals("")) {
continue;
}
if (pattern.matcher(strings[i]).matches()) {
stack.push(Double.parseDouble(strings[i]));
}
else {
double y = stack.pop();
double x = stack.pop();
stack.push(calculate(x, y, strings[i]));
}
}
return stack.pop();
}
private static Double calculate(double x, double y, String string) {
if (string.trim().equals("+")) {
return x + y;
}
if (string.trim().equals("-")) {
return x - y;
}
if (string.trim().equals("*")) {
return x * y;
}
if (string.trim().equals("/")) {
return x / y;
}
return (double) 0;
}
}
class TestDemo {
public static void main(String[] args) {
String str = "3+(8-5)*6/3";
String str2 = "3+2-5";
System.out.println(StringToArithmetic.infixToSuffix(str));
System.out.println(StringToArithmetic.stringToArithmetic(str));
}
}
|

